题目内容
7. 为了解某校九年级学生的身高情况,随机抽取部分学生的身高进行调查,利用所得数据绘成如图统计图表:
为了解某校九年级学生的身高情况,随机抽取部分学生的身高进行调查,利用所得数据绘成如图统计图表:频数分布表
| 身高分组 | 频数 | 百分比 |
| x<155 | 5 | 10% |
| 155≤x<160 | a | 20% |
| 160≤x<165 | 15 | 30% |
| 165≤x<170 | 14 | b |
| x≥170 | 6 | 12% |
| 总计 | 100% |
(2)补全频数分布直方图;
(3)该校九年级共有600名学生,估计身高不低于165cm的学生大约有多少人?
分析 (1)根据表格中的数据可以求得调查的学生总数,从而可以求得a的值,进而求得b的值;
(2)根据(1)中的a的值可以补全频数分布直方图;
(3)根据表格中的数据可以估算出该校九年级身高不低于165cm的学生大约有多少人.
解答 解:(1)由表格可得,
调查的总人数为:5÷10%=50,
∴a=50×20%=10,
b=14÷50×100%=28%,
故答案为:10,28%;
(2)补全的频数分布直方图如下图所示,
(3)600×(28%+12%)=600×40%=240(人)
即该校九年级共有600名学生,身高不低于165cm的学生大约有240人.
点评 本题考查频数分布直方图、用样本估计总体、频数分布表,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.A,B两地相距180km,新修的高速公路开通后,在A,B两地间行驶的长途客车平均车速提高了50%,而从A地到B地的时间缩短了1h.若设原来的平均车速为xkm/h,则根据题意可列方程为( )
| A. | $\frac{180}{x}$-$\frac{180}{(1+50%)x}$=1 | B. | $\frac{180}{(1+50%)x}$-$\frac{180}{x}$=1 | ||
| C. | $\frac{180}{x}$-$\frac{180}{(1-50%)x}$=1 | D. | $\frac{180}{(1-50%)x}$-$\frac{180}{x}$=1 |
2.一个正多边形的内角和为540°,则这个正多边形的每一个外角等于( )
| A. | 108° | B. | 90° | C. | 72° | D. | 60° |
12.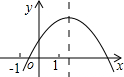 二次函数y=ax2+bx+c的图象如图所示,下列结论:
二次函数y=ax2+bx+c的图象如图所示,下列结论:
①4ac<b2;②a+c>b;③2a+b>0.
其中正确的有( )
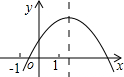 二次函数y=ax2+bx+c的图象如图所示,下列结论:
二次函数y=ax2+bx+c的图象如图所示,下列结论:①4ac<b2;②a+c>b;③2a+b>0.
其中正确的有( )
| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
19.在一个布口袋里装有白、红、黑三种颜色的小球,它们除颜色外没有任何区别,其中白球2只,红球6只,黑球4只,将袋中的球搅匀,闭上眼睛随机从袋中取出1只球,则取出黑球的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
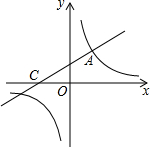 如图,直线y=$\frac{1}{2}$x+2与双曲线相交于点A(m,3),与x轴交于点C.
如图,直线y=$\frac{1}{2}$x+2与双曲线相交于点A(m,3),与x轴交于点C.