题目内容
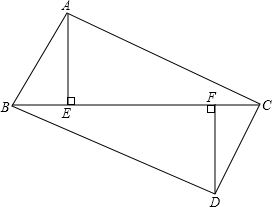 如图所示,点B、E、F、C在同一条直线上,有AE⊥BC.DF⊥BC,垂足分别为点E、F,且AC=DB,BE=CF,求证:
如图所示,点B、E、F、C在同一条直线上,有AE⊥BC.DF⊥BC,垂足分别为点E、F,且AC=DB,BE=CF,求证:(1)AC∥BD;
(2)AB∥CD.
考点:全等三角形的判定与性质,平行线的判定
专题:证明题
分析:(1)首先利用BE=CF,得出BF=CE,再由AE⊥BC,DF⊥BC,AC=DB,证得Rt△AEC≌Rt△DFB,得出∠ACE=∠DBF,证得结论;
(2)由Rt△AEC≌Rt△DFB,得出AE=DF,再由BE=CF,证得Rt△AEB≌Rt△DFC,得出∠ABE=∠DCF,证得结论.
(2)由Rt△AEC≌Rt△DFB,得出AE=DF,再由BE=CF,证得Rt△AEB≌Rt△DFC,得出∠ABE=∠DCF,证得结论.
解答:证明:(1)∵BE=CF,
∴BE+EF=CF+EF
即BF=CE,
∵AE⊥BC,DF⊥BC,
∴∠AEC=∠DFB=90°,
在Rt△AEC和Rt△DFB中,
∴Rt△AEC≌Rt△DFB(HL)
∴∠ACE=∠DBF,
∴AC∥BD;
(2)∵Rt△AEC≌Rt△DFB
∴AE=DF,
Rt△AEB≌Rt△DFC中
∴Rt△AEB≌Rt△DFC(SAS),
∴∠ABE=∠DCF,
∴AB∥CD.
∴BE+EF=CF+EF
即BF=CE,
∵AE⊥BC,DF⊥BC,
∴∠AEC=∠DFB=90°,
在Rt△AEC和Rt△DFB中,
|
∴Rt△AEC≌Rt△DFB(HL)
∴∠ACE=∠DBF,
∴AC∥BD;
(2)∵Rt△AEC≌Rt△DFB
∴AE=DF,
Rt△AEB≌Rt△DFC中
|
∴Rt△AEB≌Rt△DFC(SAS),
∴∠ABE=∠DCF,
∴AB∥CD.
点评:此题考查三角形全等的判定与性质,平行线的判定,注意充分利用已知条件,找到问题的突破口.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
 如图,在四边形ABCD中,E,F分别为AC,BD的中点,则EF与AB+CD的关系是( )
如图,在四边形ABCD中,E,F分别为AC,BD的中点,则EF与AB+CD的关系是( )| A、2EF=AB+CD |
| B、2EF>AB+CD |
| C、2EF<AB+CD |
| D、不确定 |
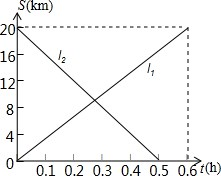 甲、乙两辆摩托车分别从A、B两地出发相向而行,图中l1、l2分别表示两辆摩托车与A地的距离s(千米)与行驶时间t(小时)之间的函数关系.
甲、乙两辆摩托车分别从A、B两地出发相向而行,图中l1、l2分别表示两辆摩托车与A地的距离s(千米)与行驶时间t(小时)之间的函数关系. 如图,以点O为圆心的两个同心圆中,大圆的弦AB、CD是小圆的两条切线,切点分别为M、N,那么AB、CD是否相等?为什么?
如图,以点O为圆心的两个同心圆中,大圆的弦AB、CD是小圆的两条切线,切点分别为M、N,那么AB、CD是否相等?为什么?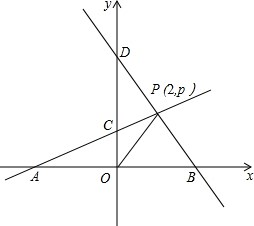 已知,A、B分别是x轴上位于原点左、右两侧的点,点P(2,p)在第一象限,直线PA交y轴于点C(0,2),直线PB交y轴于点D,S△AOP=6.
已知,A、B分别是x轴上位于原点左、右两侧的点,点P(2,p)在第一象限,直线PA交y轴于点C(0,2),直线PB交y轴于点D,S△AOP=6.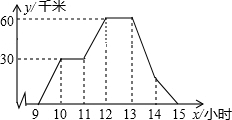 A、B两地相距60千米,图中折线表示某骑车人离A地的距离与时间的函数关系,有一辆客车9时从B地出发,以60千米/小时的速度为匀速行驶,并返往于两地之间(乘客上、下车停留时间忽略不计)
A、B两地相距60千米,图中折线表示某骑车人离A地的距离与时间的函数关系,有一辆客车9时从B地出发,以60千米/小时的速度为匀速行驶,并返往于两地之间(乘客上、下车停留时间忽略不计) 如图,直线AB、CD相交于点O.
如图,直线AB、CD相交于点O.