题目内容
 如图,在四边形ABCD中,E,F分别为AC,BD的中点,则EF与AB+CD的关系是( )
如图,在四边形ABCD中,E,F分别为AC,BD的中点,则EF与AB+CD的关系是( )| A、2EF=AB+CD |
| B、2EF>AB+CD |
| C、2EF<AB+CD |
| D、不确定 |
考点:三角形中位线定理,三角形三边关系
专题:计算题
分析:作BC的中点G,连接EG、FG,根据三角形中位线定理得到EG=
AB,FG=
CD,在△EFG中,利用三角形的三边关系即可证得.
| 1 |
| 2 |
| 1 |
| 2 |
解答: 解:作BC的中点G,连接EG、FG.
解:作BC的中点G,连接EG、FG.
∵E、G是AC和BC的中点,即EG是△ABC的中位线,
∴EG=
AB,
同理,FG=
CD,
∵在△EFG中,EF<EG+FG,
∴EF<
AB+
CD=
(AB+CD),
∴2EF<AB+CD.
故选C.
 解:作BC的中点G,连接EG、FG.
解:作BC的中点G,连接EG、FG.∵E、G是AC和BC的中点,即EG是△ABC的中位线,
∴EG=
| 1 |
| 2 |
同理,FG=
| 1 |
| 2 |
∵在△EFG中,EF<EG+FG,
∴EF<
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴2EF<AB+CD.
故选C.
点评:此题考查的是三角形中位线的性质,即三角形的中位线平行于第三边且等于第三边的一半以及三角形的三边的关系,两边之和大于第三边,正确作出BC的中点是关键.

练习册系列答案
相关题目
若关于x的一元二次方程ax2+bx+c=0(a≠0)的两根为x1,x2,则x1+x2=-
,x1•x2=
.当a=1,b=6,c=5时,x1x2+x1+x2的值是( )
| b |
| a |
| c |
| a |
| A、5 | B、-5 | C、1 | D、-1 |
 如图,在⊙O中,BC为⊙O的弦,点A在⊙O内(点O、A在弦BC的同一侧),连接OA、AB,若线段OA的长为8,线段AB的长为12,∠OAB的度数与∠ABC的度数相等,均为60°,则弦BC的长为( )
如图,在⊙O中,BC为⊙O的弦,点A在⊙O内(点O、A在弦BC的同一侧),连接OA、AB,若线段OA的长为8,线段AB的长为12,∠OAB的度数与∠ABC的度数相等,均为60°,则弦BC的长为( )| A、12 | B、15 | C、16 | D、20 |
下列四个数中,负数是( )
| A、|-2| | ||
| B、(-2)2 | ||
C、(-
| ||
D、
|
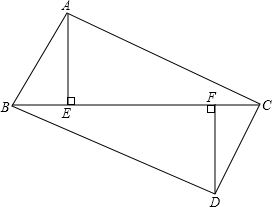 如图所示,点B、E、F、C在同一条直线上,有AE⊥BC.DF⊥BC,垂足分别为点E、F,且AC=DB,BE=CF,求证:
如图所示,点B、E、F、C在同一条直线上,有AE⊥BC.DF⊥BC,垂足分别为点E、F,且AC=DB,BE=CF,求证: