题目内容
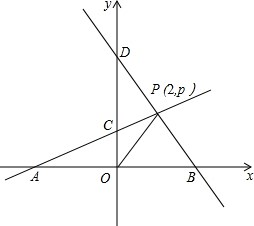 已知,A、B分别是x轴上位于原点左、右两侧的点,点P(2,p)在第一象限,直线PA交y轴于点C(0,2),直线PB交y轴于点D,S△AOP=6.
已知,A、B分别是x轴上位于原点左、右两侧的点,点P(2,p)在第一象限,直线PA交y轴于点C(0,2),直线PB交y轴于点D,S△AOP=6.(1)求△COP的面积;
(2)求点A的坐标和m的值;
(3)若S△BOP=S△DOP,求直线BD的函数解析式.
考点:两条直线相交或平行问题
专题:代数几何综合题,待定系数法
分析:(1)已知P的横坐标,即可知道△OCP的边OC上的高长,利用三角形的面积公式即可求解;
(2)求得△AOC的面积,即可求得A的坐标,利用待定系数法即可求得AP的解析式,把x=2代入解析式即可求得p的值;
(3)设直线BD的解析式为y=kx+b(a≠0),再把P(2,3)代入得出2k+b=3,故可得出D(0,b),B(-
,0),再根据三角形的面积公式即可得出结论.
(2)求得△AOC的面积,即可求得A的坐标,利用待定系数法即可求得AP的解析式,把x=2代入解析式即可求得p的值;
(3)设直线BD的解析式为y=kx+b(a≠0),再把P(2,3)代入得出2k+b=3,故可得出D(0,b),B(-
| b |
| k |
解答: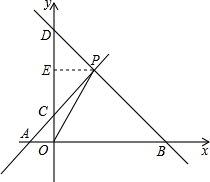 解:(1)作PE⊥y轴于E,
解:(1)作PE⊥y轴于E,
∵P的横坐标是2,则PE=2.
∴S△COP=
OC•PE=
×2×2=2;
(2)∴S△AOC=S△AOP-S△COP=6-2=4,
∴S△AOC=
OA•OC=4,即
×OA×2=4,
∴OA=4,
∴A的坐标是(-4,0).
设直线AP的解析式是y=kx+b,则
,
解得:
.
则直线的解析式是y=
x+2.
当x=2时,y=3,即m=3;
(3)设直线BD的解析式为y=ax+c(a≠0),
∵P(2,3),
∴2a+c=3,
∴D(0,c),B(-
,0),
∵S△BOP=S△DOP,
∴
OD•2=
OB•3,即c=-
,
解得a=-
,
∴c=6,
∴BD的解析式是:y=-
x+6.
 解:(1)作PE⊥y轴于E,
解:(1)作PE⊥y轴于E,∵P的横坐标是2,则PE=2.
∴S△COP=
| 1 |
| 2 |
| 1 |
| 2 |
(2)∴S△AOC=S△AOP-S△COP=6-2=4,
∴S△AOC=
| 1 |
| 2 |
| 1 |
| 2 |
∴OA=4,
∴A的坐标是(-4,0).
设直线AP的解析式是y=kx+b,则
|
解得:
|
则直线的解析式是y=
| 1 |
| 2 |
当x=2时,y=3,即m=3;
(3)设直线BD的解析式为y=ax+c(a≠0),
∵P(2,3),
∴2a+c=3,
∴D(0,c),B(-
| c |
| a |
∵S△BOP=S△DOP,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 3c |
| 2a |
解得a=-
| 3 |
| 2 |
∴c=6,
∴BD的解析式是:y=-
| 3 |
| 2 |
点评:本题考查了三角形的面积与一次函数待定系数求函数解析式的综合应用,正确求得A的坐标是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
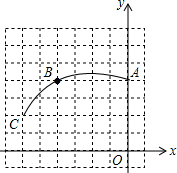 如图,在正方形网格图中建立平面直角坐标系,一条圆弧经过网格点A(0,4)、B(-4,4)、C(-6,2),请在网格图中进行如下操作:
如图,在正方形网格图中建立平面直角坐标系,一条圆弧经过网格点A(0,4)、B(-4,4)、C(-6,2),请在网格图中进行如下操作: 如图,已知直线y=x+m与双曲线y=
如图,已知直线y=x+m与双曲线y= 已知,如图,点E、F分别为四边形ABCD的对角线AC、BD的中点,求证:EF<
已知,如图,点E、F分别为四边形ABCD的对角线AC、BD的中点,求证:EF<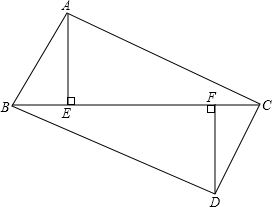 如图所示,点B、E、F、C在同一条直线上,有AE⊥BC.DF⊥BC,垂足分别为点E、F,且AC=DB,BE=CF,求证:
如图所示,点B、E、F、C在同一条直线上,有AE⊥BC.DF⊥BC,垂足分别为点E、F,且AC=DB,BE=CF,求证: 如图,等腰梯形ABCD中,AB∥CD,AB=2,CD=4,A(0,3),直线y=ax+b过B、C两点,反比例函数
如图,等腰梯形ABCD中,AB∥CD,AB=2,CD=4,A(0,3),直线y=ax+b过B、C两点,反比例函数