题目内容
 如图,直线AB、CD相交于点O.
如图,直线AB、CD相交于点O.(1)若∠AOC+∠BOD=100°,求各角的度数.
(2)若∠BOC比∠AOC的两倍多33°,求各角的度数.
考点:对顶角、邻补角
专题:计算题
分析:(1)根据对顶角相等,邻补角互补,∠AOC+∠BOD=100°,可得答案;
(2)根据邻补角互补,∠BOC比∠AOC的倍多33°可得,∠BOC与∠AOC的大小,根据对顶角相等,可得答案.
(2)根据邻补角互补,∠BOC比∠AOC的倍多33°可得,∠BOC与∠AOC的大小,根据对顶角相等,可得答案.
解答:解:(1)由对顶角相等得∠AOC=∠BOD,
∠AOC=∠BOD=55°,
由邻补角互补得∠BOC=180°-∠AOC=180°-55°=125°,
由邻补角互补得∠AOD=180°-∠AOC=180°-55=125°;
(2)由邻补角角的性质,得∠BOC+∠AOC=180°,
由∠BOC比∠AOC的两倍多33°,得
∠BOC=2∠AOC+33°
2∠AOC+33°+∠AOC=180°
∠AOC=49°,
由对顶角相等得∠BOD=∠AOC=49°,
由邻补角互补得∠BOC=180-∠AOC=180°-49°=131°,
由对顶角相等得∠AOD=∠BOC=131°.
∠AOC=∠BOD=55°,
由邻补角互补得∠BOC=180°-∠AOC=180°-55°=125°,
由邻补角互补得∠AOD=180°-∠AOC=180°-55=125°;
(2)由邻补角角的性质,得∠BOC+∠AOC=180°,
由∠BOC比∠AOC的两倍多33°,得
∠BOC=2∠AOC+33°
2∠AOC+33°+∠AOC=180°
∠AOC=49°,
由对顶角相等得∠BOD=∠AOC=49°,
由邻补角互补得∠BOC=180-∠AOC=180°-49°=131°,
由对顶角相等得∠AOD=∠BOC=131°.
点评:本题考查了对顶角、邻补角,(1)对顶角相等,邻补角互补,(2)由邻补角互补,两角的关系,得出两个二元一次方程,解二元一次方程组,再由对顶角相等,邻补角互补得出答案.

练习册系列答案
相关题目
 如图,OA=OB,OC=OD,∠AOC=∠BOD=90°,M、N分别是AC、BD的中点,连接MN、ON,求证:MN=
如图,OA=OB,OC=OD,∠AOC=∠BOD=90°,M、N分别是AC、BD的中点,连接MN、ON,求证:MN=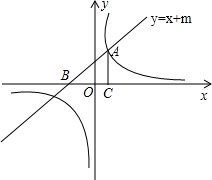 如图,已知直线y=x+m与双曲线y=
如图,已知直线y=x+m与双曲线y=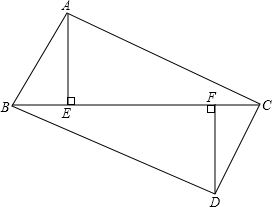 如图所示,点B、E、F、C在同一条直线上,有AE⊥BC.DF⊥BC,垂足分别为点E、F,且AC=DB,BE=CF,求证:
如图所示,点B、E、F、C在同一条直线上,有AE⊥BC.DF⊥BC,垂足分别为点E、F,且AC=DB,BE=CF,求证: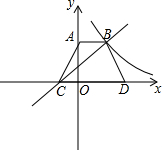 如图,等腰梯形ABCD中,AB∥CD,AB=2,CD=4,A(0,3),直线y=ax+b过B、C两点,反比例函数
如图,等腰梯形ABCD中,AB∥CD,AB=2,CD=4,A(0,3),直线y=ax+b过B、C两点,反比例函数 如图,DH∥EO∥BC,EF∥CD,则与∠BFE相等的角,不包括∠BFE有
如图,DH∥EO∥BC,EF∥CD,则与∠BFE相等的角,不包括∠BFE有 如图,在⊙O中,BC为⊙O的弦,点A在⊙O内(点O、A在弦BC的同一侧),连接OA、AB,若线段OA的长为8,线段AB的长为12,∠OAB的度数与∠ABC的度数相等,均为60°,则弦BC的长为( )
如图,在⊙O中,BC为⊙O的弦,点A在⊙O内(点O、A在弦BC的同一侧),连接OA、AB,若线段OA的长为8,线段AB的长为12,∠OAB的度数与∠ABC的度数相等,均为60°,则弦BC的长为( )