题目内容
观察下列等式:
=1-
,
=
-
,
=
-
,将以上三个等式两边分别相加得:
+
+
=1-
+
-
+
-
=1-
=
(1)猜想并写出
=
(2)直接写出下列各式的计算结果:
①
+
+
+…+
=
②
+
+
+…+…
=
(3)探究并计算:
+
+
+…+
.
| 1 |
| 1×2 |
| 1 |
| 2 |
| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
(1)猜想并写出
| 1 |
| n(n+1) |
(2)直接写出下列各式的计算结果:
①
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 2010×2011 |
②
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| n(n+1) |
(3)探究并计算:
| 1 |
| 2×4 |
| 1 |
| 4×6 |
| 1 |
| 6×8 |
| 1 |
| 2010×2012 |
考点:有理数的混合运算
专题:规律型
分析:(1)先根据题中所给出的列子进行猜想,写出猜想结果即可;
(2)根据(1)中的猜想计算出结果;
(3)根据乘法分配律提取
,再计算即可求解.
(2)根据(1)中的猜想计算出结果;
(3)根据乘法分配律提取
| 1 |
| 4 |
解答:解:(1)
=
-
;
(2)直接写出下列各式的计算结果:
①
+
+
+…+
=1-
+
-
+…+
-
=1-
=
;
②
+
+
+…+…
=1-
+
-
+…+
-
=1-
=
;
(3)
+
+
+…+
=
×(
+
+
+…+
)
═
×
=
.
故答案为:
-
;
;
.
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
(2)直接写出下列各式的计算结果:
①
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 2010×2011 |
=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2010 |
| 1 |
| 2011 |
=1-
| 1 |
| 2011 |
=
| 2010 |
| 2011 |
②
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| n(n+1) |
=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
=1-
| 1 |
| n+1 |
=
| n |
| n+1 |
(3)
| 1 |
| 2×4 |
| 1 |
| 4×6 |
| 1 |
| 6×8 |
| 1 |
| 2010×2012 |
=
| 1 |
| 4 |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 1005×1006 |
═
| 1 |
| 4 |
| 1005 |
| 1006 |
=
| 1005 |
| 4024 |
故答案为:
| 1 |
| n |
| 1 |
| n+1 |
| 2010 |
| 2011 |
| n |
| n+1 |
点评:本题考查的是有理数的混合运算,根据题意找出规律是解答此题的关键.

练习册系列答案
相关题目
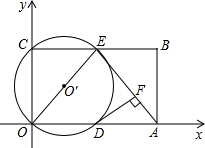 如图,在平面直角坐标系中,矩形ABCO的面积为15,边OA比OC大2.E为BC的中点,以OE为直径的⊙O′交x轴于D点,过点D作DF⊥AE于点F.
如图,在平面直角坐标系中,矩形ABCO的面积为15,边OA比OC大2.E为BC的中点,以OE为直径的⊙O′交x轴于D点,过点D作DF⊥AE于点F.
 如图所示,OE为∠AOD的平分线,∠COD=
如图所示,OE为∠AOD的平分线,∠COD= 由平面上一点A作⊙O的两条切线,切点分别为B,C.D为劣弧BC上任意一点,过D作AD的垂线交∠BOD和∠DOC的角平分线于点E和点F.求证:DE=DF.
由平面上一点A作⊙O的两条切线,切点分别为B,C.D为劣弧BC上任意一点,过D作AD的垂线交∠BOD和∠DOC的角平分线于点E和点F.求证:DE=DF.