题目内容
计算下列各式,并且把结果化成只含有正整数指数幂的形式:
(1)(-
xy)-3÷(
x2y3)-2;
(2)(3m2n-2)2•(-4mn-3)-3;
(3)(
xy)-2÷(
x-2);
(4)(
)2•(
)÷(-
)-4.
(1)(-
| 3 |
| 2 |
| 5 |
| 2 |
(2)(3m2n-2)2•(-4mn-3)-3;
(3)(
| 2 |
| 3 |
| 1 |
| 3 |
(4)(
| c2 |
| a2b |
| b2c |
| a4 |
| b2 |
| ca2 |
考点:负整数指数幂
专题:
分析:根据运算顺序,先算乘方,再算乘除即可.
解答:解:(1)原式=(-
)-3x-3y-3÷(
)-2x-4y-6
=-
÷
xy3
=-
xy3;
(2)原式=9m4n-4•(-
m-3n9);
=-
mn5;
(3)原式=(-
)-2x-2y-2÷(
)-2x-2
=
÷9y-2
=
y-2
=
;
(4)原式=
•
•
=
.
| 3 |
| 2 |
| 5 |
| 2 |
=-
| 8 |
| 27 |
| 4 |
| 25 |
=-
| 50 |
| 27 |
(2)原式=9m4n-4•(-
| 1 |
| 64 |
=-
| 9 |
| 64 |
(3)原式=(-
| 2 |
| 3 |
| 1 |
| 3 |
=
| 9 |
| 4 |
=
| 1 |
| 4 |
=
| 1 |
| 4y2 |
(4)原式=
| c4 |
| a4b2 |
| b2c |
| a4 |
| a8c4 |
| b8 |
=
| c9 |
| b8 |
点评:本题考查了负整数指数幂的运算,是基础题比较简单.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,AD、BC交于点O,P为AB、CD延长线的交点,且PA•PB=PC•PD.试说明:△PAD∽△PCB.
如图,AD、BC交于点O,P为AB、CD延长线的交点,且PA•PB=PC•PD.试说明:△PAD∽△PCB.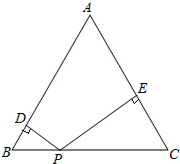 如图所示,等边三角形的高为a,P为BC边上(与BC不重合)的任意一点,且PD⊥AB于点D,PE⊥AC于E,则PE+PD=
如图所示,等边三角形的高为a,P为BC边上(与BC不重合)的任意一点,且PD⊥AB于点D,PE⊥AC于E,则PE+PD= 如图,直线EF,CD相交于点O,∠AOB=90°,且OD平分∠AOF,∠BOE=2∠AOE,求∠EOD的度数.
如图,直线EF,CD相交于点O,∠AOB=90°,且OD平分∠AOF,∠BOE=2∠AOE,求∠EOD的度数.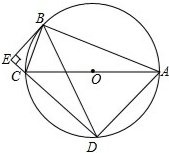 如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,弦BD=BA,BC=5,BE⊥DC交DC的延长线于点E.
如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,弦BD=BA,BC=5,BE⊥DC交DC的延长线于点E.  如图,圆内接四边形ABCD中,AC、BD相交于E,且AE=CE,求证:
如图,圆内接四边形ABCD中,AC、BD相交于E,且AE=CE,求证: