题目内容
△ABC内接于圆O,AB=AC,过点A作一直线与直线BC交于点D,与圆交于点E.
(1)如图,当点D在线段BC上时,找出图中所有相似三角形并说明AC,AD,AE之间的关系;
(2)如图,当点D在BC的延长线上时,说明AC,AD,AE之间的关系.
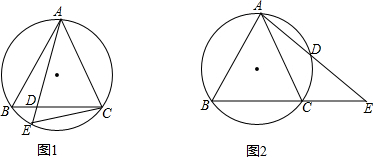
(1)如图,当点D在线段BC上时,找出图中所有相似三角形并说明AC,AD,AE之间的关系;
(2)如图,当点D在BC的延长线上时,说明AC,AD,AE之间的关系.

考点:相似三角形的判定与性质,圆周角定理
专题:
分析:(1)利用圆周角定理可得∠DAE=∠DCE,结合对顶角可得△ABD∽△CED,结合条件可得∠AEC=∠ABC=∠ACD,结合公共角,可得△ADC∽△ACE,可得到
=
,可得到AC2=AD•AE;
(2)连接CD,可得∠ADC+∠B=∠ACE+∠ACB,可得到∠ADC=∠ACE,可证得△ADC∽△ACE,可得
=
,可得出结论.
| AD |
| AC |
| AC |
| AE |
(2)连接CD,可得∠ADC+∠B=∠ACE+∠ACB,可得到∠ADC=∠ACE,可证得△ADC∽△ACE,可得
| AD |
| AC |
| AC |
| AE |
解答:解:(1)∵AB=AC,
∴∠ABC=∠ACB=∠AEC,且∠DAC=∠CAE,∠ADB=∠EDC,
∴△ABD∽△CED,△ADC∽△ACE,
∴
=
,
∴AC2=AD•AE,
综上可知相似三角形有△ABD∽△CED,△ADC∽△ACE,
AC,AD,AE之间的关系为:AC2=AD•AE;
(2)连接CD,
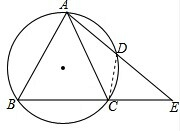
∵AB=AC,
∴∠B=∠ACB,
∵∠ADC+∠B=∠ACB+∠ACE=180°,
∴∠ADC=∠ACE,且∠DAC=∠CAE,
∴,△ADC∽△ACE,
∴
=
,
∴AC2=AD•AE.
∴∠ABC=∠ACB=∠AEC,且∠DAC=∠CAE,∠ADB=∠EDC,
∴△ABD∽△CED,△ADC∽△ACE,
∴
| AD |
| AC |
| AC |
| AE |
∴AC2=AD•AE,
综上可知相似三角形有△ABD∽△CED,△ADC∽△ACE,
AC,AD,AE之间的关系为:AC2=AD•AE;
(2)连接CD,

∵AB=AC,
∴∠B=∠ACB,
∵∠ADC+∠B=∠ACB+∠ACE=180°,
∴∠ADC=∠ACE,且∠DAC=∠CAE,
∴,△ADC∽△ACE,
∴
| AD |
| AC |
| AC |
| AE |
∴AC2=AD•AE.
点评:本题主要考查相似三角形的判定和性质,掌握相似三角形的判定方法是解题的关键,注意利用圆周角定理和圆内接四边形的性质寻找角相等.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
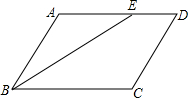 如图,在四边形ABCD中,已知BE平分∠ABC,交AD于E,∠AEB=∠ABE.
如图,在四边形ABCD中,已知BE平分∠ABC,交AD于E,∠AEB=∠ABE.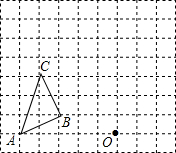 如图,在边长为1个单位长度的小正方形组成的网格中,按要求画出△A1B1C1和△A2B2C2:
如图,在边长为1个单位长度的小正方形组成的网格中,按要求画出△A1B1C1和△A2B2C2: