题目内容
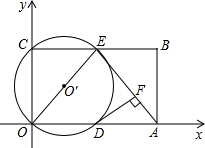 如图,在平面直角坐标系中,矩形ABCO的面积为15,边OA比OC大2.E为BC的中点,以OE为直径的⊙O′交x轴于D点,过点D作DF⊥AE于点F.
如图,在平面直角坐标系中,矩形ABCO的面积为15,边OA比OC大2.E为BC的中点,以OE为直径的⊙O′交x轴于D点,过点D作DF⊥AE于点F.(1)求OA、OC的长;
(2)求证:DF为⊙O′的切线;
(3)直线BC上存不存在除点E以外的点P,使△AOP也是等腰三角形?如果不存在,说明理由;如果存在,直接写出P点的坐标.
考点:圆的综合题
专题:
分析:(1)利用边OA比OC大2且面积为15,可列方程求得OA、OC;
(2)连接O′D,由条件可证明△OCE≌△ABE,可得到EO=EA,得到∠1=∠2=∠3,可得到∠3+∠ADF=90°,从而可得到∠O′DF=90°,可证得结论;
(3)分别以点A、点O为圆心,OA为半径画圆,与BC的交点即为满足条件的P点,结合勾股定理可求得这些点的坐标.
(2)连接O′D,由条件可证明△OCE≌△ABE,可得到EO=EA,得到∠1=∠2=∠3,可得到∠3+∠ADF=90°,从而可得到∠O′DF=90°,可证得结论;
(3)分别以点A、点O为圆心,OA为半径画圆,与BC的交点即为满足条件的P点,结合勾股定理可求得这些点的坐标.
解答:(1)解:在矩形OABC中,设OC=x,则OA=x+2,
∴x(x+2)=15,
∴x1=3,x2=-5,
∴x2=-5(不合题意,舍去),
∴OC=3,OA=5;
(2)证明:如图1,连接O′D,
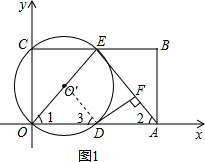
在矩形OABC中,OC=AB,∠OCB=∠ABC=90°,CE=BE=
,
在△OCE和△ABE中,
,
∴△0CE≌△ABE(SAS),
∴EA=EO,
∴∠1=∠2;
∵在⊙O′中,O′O=O′D,
∴∠1=∠3,
∴∠3=∠2,
∴O′D∥AE;
∵DF⊥AE,
∴DF⊥O′D,
∵点D在⊙O′上,O′D为⊙O′的半径,
∴DF为⊙O′切线;
(3)解:存在.
①当A0=AP时,如图2,以点A为圆心,以AO为半径画弧交BC于P1和P4两点
过P1点作P1H⊥OA于点H,P1H=0C=3;
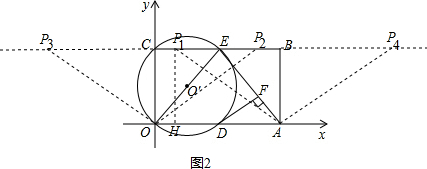
∵APl=OA=5,
∴AH=4,
∴OH=l,
求得点P1(1,3)同理可得:P4(9,3);
②当OA=OP时,同上可求得P2(4,3),P3(-4,3),
∴在直线BC上,除了E点外,既存在⊙O′内的点P,又存在⊙O′外的点P使△AOP为等腰三角形,
其坐标为(1,3)或(9,3)或(4,3)或(-4,3).
∴x(x+2)=15,
∴x1=3,x2=-5,
∴x2=-5(不合题意,舍去),
∴OC=3,OA=5;
(2)证明:如图1,连接O′D,

在矩形OABC中,OC=AB,∠OCB=∠ABC=90°,CE=BE=
| 5 |
| 2 |
在△OCE和△ABE中,
|
∴△0CE≌△ABE(SAS),
∴EA=EO,
∴∠1=∠2;
∵在⊙O′中,O′O=O′D,
∴∠1=∠3,
∴∠3=∠2,
∴O′D∥AE;
∵DF⊥AE,
∴DF⊥O′D,
∵点D在⊙O′上,O′D为⊙O′的半径,
∴DF为⊙O′切线;
(3)解:存在.
①当A0=AP时,如图2,以点A为圆心,以AO为半径画弧交BC于P1和P4两点
过P1点作P1H⊥OA于点H,P1H=0C=3;

∵APl=OA=5,
∴AH=4,
∴OH=l,
求得点P1(1,3)同理可得:P4(9,3);
②当OA=OP时,同上可求得P2(4,3),P3(-4,3),
∴在直线BC上,除了E点外,既存在⊙O′内的点P,又存在⊙O′外的点P使△AOP为等腰三角形,
其坐标为(1,3)或(9,3)或(4,3)或(-4,3).
点评:本题主要考查切线的判定和矩形的性质、等腰三角形的判定及勾股定理等知识的综合应用.在(1)中注意方程思想的应用;在(2)中注意证明切线的两种方法,即有切点时连接圆心和切点,证明垂直,没有切点时作垂直,证明距离等于半径;在(3)中注意利用圆上的点到圆心的距离相等的特点找出满足条件的点的位置.本题综合性较强,待查知识点较多,在平时的学习中要注意知识的灵活运用.

练习册系列答案
相关题目
 有理数a在数轴上位置如图,则下列结论中正确的是( )
有理数a在数轴上位置如图,则下列结论中正确的是( )| A、a+3是正数 |
| B、a+3是负数 |
| C、a-3是正数 |
| D、a-3为0 |
 如图,直线EF,CD相交于点O,∠AOB=90°,且OD平分∠AOF,∠BOE=2∠AOE,求∠EOD的度数.
如图,直线EF,CD相交于点O,∠AOB=90°,且OD平分∠AOF,∠BOE=2∠AOE,求∠EOD的度数.