题目内容
如图所示，OE为∠AOD的平分线，∠COD=| 1 |
| 4 |
考点：角平分线的定义
专题：
分析：根据角平分线的性质可得∠AOD=∠AOE=2∠DOE，设∠COD=x°，根据∠COD=
∠EOC可得∠DOE=3x°，∠AOE=3x°，再利用方程可得3x=60°，计算出x的值，然后可得∠AOC的度数．
| 1 |
| 4 |
解答：解：∵OE为∠AOD的平分线，
∴∠AOD=∠AOE=2∠DOE，
设∠COD=x°，则∠DOE=3x°，∠AOE=3x°，
∵∠AOE=60°，
∴3x=60°，
∴x=20°，
∴∠AOC=7x°=140°．
∴∠AOD=∠AOE=2∠DOE，
设∠COD=x°，则∠DOE=3x°，∠AOE=3x°，
∵∠AOE=60°，
∴3x=60°，
∴x=20°，
∴∠AOC=7x°=140°．
点评：此题主要考查了角平分线的性质，以及角的计算，关键是掌握方程思想的应用．
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
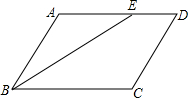如图，在四边形ABCD中，已知BE平分∠ABC，交AD于E，∠AEB=∠ABE．
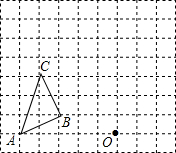如图，在边长为1个单位长度的小正方形组成的网格中，按要求画出△A1B1C1和△A2B2C2：
有理数a在数轴上位置如图，则下列结论中正确的是（ ）| A、a+3是正数 |
| B、a+3是负数 |
| C、a-3是正数 |
| D、a-3为0 |