题目内容
 由平面上一点A作⊙O的两条切线,切点分别为B,C.D为劣弧BC上任意一点,过D作AD的垂线交∠BOD和∠DOC的角平分线于点E和点F.求证:DE=DF.
由平面上一点A作⊙O的两条切线,切点分别为B,C.D为劣弧BC上任意一点,过D作AD的垂线交∠BOD和∠DOC的角平分线于点E和点F.求证:DE=DF.考点:切线的性质
专题:证明题
分析:连接FC,DC,过C作DF的平行线,与OF交于G,过F作FH∥OC,可证得△ADC∽△CGO,结合条件进一步可证得△ACO∽△AFD和△AED∽△AOB,可证得∠DAF=∠EAD,结合AD⊥EF,可证得结论.
解答: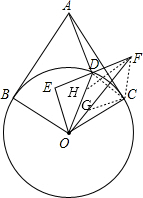 证明:连接FC,DC,过C作DF的平行线,与OF交于G,过F作FH∥OC,
证明:连接FC,DC,过C作DF的平行线,与OF交于G,过F作FH∥OC,
∵FH∥OC,∠ACO=90°,且AD⊥DF,
∴∠DAC=∠DFH,
∵∠ACD=∠FOC,
∴△ADC∽△CGO,
∴
=
,
∴
=
,
∵OF平分∠DOC,OD=OC,CG∥DF,
∴DF=DC=CG,
∴
=
,
又∵∠ADF=∠ACO=90°,
∴△ACO∽△AFD,
∴∠OAC=∠DAF,
同理:△AED∽△AOB,
∴∠BAO=∠EAD,
∵∠BAO=∠CAO,
∴∠DAF=∠EAD,
∵AD⊥EF,
∴ED=FD.
 证明:连接FC,DC,过C作DF的平行线,与OF交于G,过F作FH∥OC,
证明:连接FC,DC,过C作DF的平行线,与OF交于G,过F作FH∥OC,∵FH∥OC,∠ACO=90°,且AD⊥DF,
∴∠DAC=∠DFH,
∵∠ACD=∠FOC,
∴△ADC∽△CGO,
∴
| AC |
| AD |
| OC |
| CG |
∴
| CG |
| AD |
| OC |
| AC |
∵OF平分∠DOC,OD=OC,CG∥DF,
∴DF=DC=CG,
∴
| DF |
| AD |
| OC |
| OA |
又∵∠ADF=∠ACO=90°,
∴△ACO∽△AFD,
∴∠OAC=∠DAF,
同理:△AED∽△AOB,
∴∠BAO=∠EAD,
∵∠BAO=∠CAO,
∴∠DAF=∠EAD,
∵AD⊥EF,
∴ED=FD.
点评:本题主要考查相似三角形的判定和性质及切线的性质,通过作平行构造三角形相似是解题的关键,注意利用相似来寻找角相等是解题的常用思路.

练习册系列答案
相关题目
 有理数a在数轴上位置如图,则下列结论中正确的是( )
有理数a在数轴上位置如图,则下列结论中正确的是( )| A、a+3是正数 |
| B、a+3是负数 |
| C、a-3是正数 |
| D、a-3为0 |
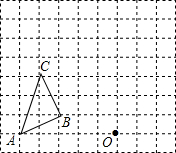 如图,在边长为1个单位长度的小正方形组成的网格中,按要求画出△A1B1C1和△A2B2C2:
如图,在边长为1个单位长度的小正方形组成的网格中,按要求画出△A1B1C1和△A2B2C2: