题目内容
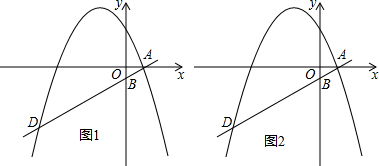
如图,在平面直角坐标系xOy中,直线y=
x-
交x轴于点A,交y轴于点B,经过点A的抛物线y=
x2+bx+c交直线AB另一点D,且点D到y轴的距离为8.
(1)求抛物线解析式;
(2)点P是直线AD上方的抛物线上一动点,(不与点A、D重合),过点P作PE⊥AD于E,过点P作PF∥y轴交AD于F,设△PEF的周长为L,点P的坐标为m,求L与m的函数关系式,并直接写出自变量m的取值范围;
(3)在图(2)的条件下,当L最大时,连接PD.将△PED沿射线PE方向平移,点P、E、F的对应点分别为Q、M、N,当△QMN的顶点M在抛物线上时,求M点的横坐标,并判断此时点N是否在直线PF上.
(参考公式:二次函数y=ax2+bx+c(c≠0).当x=-
时,y最大(小)值=
)
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 4 |
(1)求抛物线解析式;
(2)点P是直线AD上方的抛物线上一动点,(不与点A、D重合),过点P作PE⊥AD于E,过点P作PF∥y轴交AD于F,设△PEF的周长为L,点P的坐标为m,求L与m的函数关系式,并直接写出自变量m的取值范围;
(3)在图(2)的条件下,当L最大时,连接PD.将△PED沿射线PE方向平移,点P、E、F的对应点分别为Q、M、N,当△QMN的顶点M在抛物线上时,求M点的横坐标,并判断此时点N是否在直线PF上.
(参考公式:二次函数y=ax2+bx+c(c≠0).当x=-
| b |
| 2a |
| 4ac-b2 |
| 4a |

考点:二次函数综合题
专题:
分析:(1)根据题意得出D点坐标,进而利用待定系数法求二次函数解析式即可;
(2)利用B(0,-
),D(-8,-
),则OB=
,OC=
,得出BC=6,设点P与F的横坐标为m,∠PFE=∠DBC,则P(m,
m2-
m+
),F(m,
m-
),由
=
,求出即可;
(3)利用配方法得出P(-3,
),PK=
,PF=
,则KF=
,利用△OAB∽△KAF,以及△PEF∽△BCD,进而得出点B,E重合,即可得出M点横坐标进而得出答案.
(2)利用B(0,-
| 3 |
| 2 |
| 15 |
| 2 |
| 3 |
| 2 |
| 15 |
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
| 5 |
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| L |
| △BCD的周长 |
| PF |
| BD |
(3)利用配方法得出P(-3,
| 5 |
| 2 |
| 5 |
| 2 |
| 25 |
| 4 |
| 15 |
| 4 |
解答: 解:(1)由题意知:A(2,0),B(0,-
解:(1)由题意知:A(2,0),B(0,-
),
过D作DC⊥y轴于C,则DC=8,
∴点D在y=
x-
上,
∴y=
×(-8)-
=-
,
∴D(-8,-
),
∵点A(2,0),D(-8,-
)在抛物线上,
∴
,
解得:
,
∴抛物线解析式为:y=-
x2-
x+
;
(2)∵B(0,-
),D(-8,-
),
∴OB=
,OC=
,
∴BC=6,在Rt△BCD中,BD=10,△BCD的周长为24,
∵PF∥y轴,
∴点P与F的横坐标为m,∠PFE=∠DBC,
∴P(m,
m2-
m+
),F(m,
m-
),
∴PF=-
m2-
m+4,
∵PE⊥AD,DC⊥y轴,
∴
=
,
L=-
m2-
m+
(-8<m<2);
(3)L=-
m2-
m+
=-
(m+3)2+15,
∵-
<0,
∴当m=-3,L最大,
∴P(-3,
),PK=
,PF=
,
∴KF=
,
∵A(2,0),B(0,-
),
∴OA=2,OB=
,
在Rt△OAB中,AB=
=
,
∵OB∥FK,
∴△OAB∽△KAF,
∴
=
,
∴AF=
,∴BP=
,
∵△PEF∽△BCD,
∴
=
,
∴EF=
,
∴点B,E重合,
∵P(-3,
),B(0,-
),
∴直线PB的解析式为:y=-
x-
,
则令M点坐标为:(n,-
n-
),
点M在抛物线y=-
x2-
x+
上,
∴-
n-
=-
n2-
n+
,
整理得:(n+3)(3n-16)=0,
解得;n1=-3(舍去),n2=
,
∴M点横坐标为:
,
∵点E的横坐标为0,M点横坐标为:
,
∴△PED向右平移了
个单位长度,
∴点D也向右平移了
个单位长度,
∴点N的横坐标为:-8+
≠-3,
又∵直线PF上点的横坐标为:-3,
∴点N不在直线PF上.
 解:(1)由题意知:A(2,0),B(0,-
解:(1)由题意知:A(2,0),B(0,-| 3 |
| 2 |
过D作DC⊥y轴于C,则DC=8,
∴点D在y=
| 3 |
| 4 |
| 3 |
| 2 |
∴y=
| 3 |
| 4 |
| 3 |
| 2 |
| 15 |
| 2 |
∴D(-8,-
| 15 |
| 2 |
∵点A(2,0),D(-8,-
| 15 |
| 2 |
∴
|
解得:
|
∴抛物线解析式为:y=-
| 1 |
| 4 |
| 3 |
| 4 |
| 5 |
| 2 |
(2)∵B(0,-
| 3 |
| 2 |
| 15 |
| 2 |
∴OB=
| 3 |
| 2 |
| 15 |
| 2 |
∴BC=6,在Rt△BCD中,BD=10,△BCD的周长为24,
∵PF∥y轴,
∴点P与F的横坐标为m,∠PFE=∠DBC,
∴P(m,
| 1 |
| 4 |
| 3 |
| 4 |
| 5 |
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
∴PF=-
| 1 |
| 4 |
| 3 |
| 2 |
∵PE⊥AD,DC⊥y轴,
∴
| L |
| △BCD的周长 |
| PF |
| BD |
L=-
| 3 |
| 5 |
| 18 |
| 5 |
| 48 |
| 5 |
(3)L=-
| 3 |
| 5 |
| 18 |
| 5 |
| 48 |
| 5 |
| 3 |
| 5 |
∵-
| 3 |
| 5 |
∴当m=-3,L最大,
∴P(-3,
| 5 |
| 2 |
| 5 |
| 2 |
| 25 |
| 4 |
∴KF=
| 15 |
| 4 |
∵A(2,0),B(0,-
| 3 |
| 2 |
∴OA=2,OB=
| 3 |
| 2 |
在Rt△OAB中,AB=
| OA2+OB2 |
| 5 |
| 2 |
∵OB∥FK,
∴△OAB∽△KAF,
∴
| AB |
| AF |
| OB |
| KF |
∴AF=
| 25 |
| 4 |
| 15 |
| 4 |
∵△PEF∽△BCD,
∴
| EF |
| BC |
| PF |
| BD |
∴EF=
| 15 |
| 4 |
∴点B,E重合,
∵P(-3,
| 5 |
| 2 |
| 3 |
| 2 |
∴直线PB的解析式为:y=-
| 4 |
| 3 |
| 3 |
| 2 |
则令M点坐标为:(n,-
| 4 |
| 3 |
| 3 |
| 2 |
点M在抛物线y=-
| 1 |
| 4 |
| 3 |
| 4 |
| 5 |
| 2 |
∴-
| 4 |
| 3 |
| 3 |
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
| 5 |
| 2 |
整理得:(n+3)(3n-16)=0,
解得;n1=-3(舍去),n2=
| 16 |
| 3 |
∴M点横坐标为:
| 16 |
| 3 |
∵点E的横坐标为0,M点横坐标为:
| 16 |
| 3 |
∴△PED向右平移了
| 16 |
| 3 |
∴点D也向右平移了
| 16 |
| 3 |
∴点N的横坐标为:-8+
| 16 |
| 3 |
又∵直线PF上点的横坐标为:-3,
∴点N不在直线PF上.
点评:此题主要考查了二次函数综合以及相似三角形的判定与性质以及图形的平移等知识,得出M点横坐标是解题关键.

练习册系列答案
相关题目
 如图,E是长方形ABCD的边AB上的点,EF⊥DE交BC于点F
如图,E是长方形ABCD的边AB上的点,EF⊥DE交BC于点F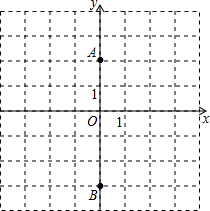 如图,A(0,2),B(0,-3),△ABC的面积为5,点C在x轴上,求点C的坐标.
如图,A(0,2),B(0,-3),△ABC的面积为5,点C在x轴上,求点C的坐标. 如图,已知直线
如图,已知直线 某校为了了解九年级男生立定跳远的成绩,从该校随机抽取了50名男生的测试成绩,根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成下面的扇形图和统计表:
某校为了了解九年级男生立定跳远的成绩,从该校随机抽取了50名男生的测试成绩,根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成下面的扇形图和统计表: