题目内容
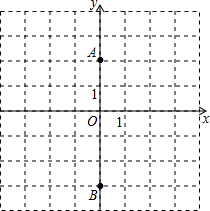 如图,A(0,2),B(0,-3),△ABC的面积为5,点C在x轴上,求点C的坐标.
如图,A(0,2),B(0,-3),△ABC的面积为5,点C在x轴上,求点C的坐标.考点:坐标与图形性质,三角形的面积
专题:
分析:设点C的坐标为(x,0),根据点的坐标得到BA=5,BA上的高为|x|,然后根据三角形面积公式列出方程,解方程即可.
解答:解:设点C的坐标为(x,0),
∵A(0,2),B(0,-3),
∴BA=5,BA上的高为|x|.
∵△ABC的面积为5,
∴
×5×|x|=5,
∴|x|=2,
∴x=±2,
故点C的坐标为(2,0)或(-2,0).
∵A(0,2),B(0,-3),
∴BA=5,BA上的高为|x|.
∵△ABC的面积为5,
∴
| 1 |
| 2 |
∴|x|=2,
∴x=±2,
故点C的坐标为(2,0)或(-2,0).
点评:本题考查了三角形面积公式:三角形的面积等于底边长与高线乘积的一半,即S△=
×底×高.也考查了坐标与图形性质.
| 1 |
| 2 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知∠1与∠2互补,∠2与∠3互补,那么∠1与∠3的关系是( )
| A、相等 | B、互补 |
| C、互余 | D、不能确定 |

 如图,已知AB∥CD,E是AB上一点,DE平分∠BEC交CD于点D,∠BEC=100°,则∠D=
如图,已知AB∥CD,E是AB上一点,DE平分∠BEC交CD于点D,∠BEC=100°,则∠D=