题目内容
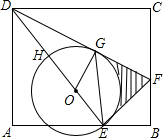 如图,E是长方形ABCD的边AB上的点,EF⊥DE交BC于点F
如图,E是长方形ABCD的边AB上的点,EF⊥DE交BC于点F(1)求证:△ADE∽△BEF;
(2)设H是ED上一点,以EH为直径作⊙O,DF与⊙O相切于点G,若DH=OH=3,求图中阴影部分的面积(结果保留到小数点后面第一位,
| 3 |
考点:切线的性质,矩形的性质,扇形面积的计算,相似三角形的判定,特殊角的三角函数值
专题:综合题
分析:(1)由条件可证∠AED=∠EFB,从而可证△ADE∽△BEF.
(2)由DF与⊙O相切,DH=OH=OG=3可得∠ODG=30°,从而有∠GOE=120°,并可求出DG、EF长,从而可以求出△DGO、△DEF、扇形OEG的面积,进而可以求出图中阴影部分的面积.
(2)由DF与⊙O相切,DH=OH=OG=3可得∠ODG=30°,从而有∠GOE=120°,并可求出DG、EF长,从而可以求出△DGO、△DEF、扇形OEG的面积,进而可以求出图中阴影部分的面积.
解答:(1)证明:∵四边形ABCD是矩形,
∴∠A=∠B=90°.
∵EF⊥DE,
∴∠DEF=90°.
∴∠AED=90°-∠BEF=∠EFB.
∵∠A=∠B,∠AED=∠EFB,
∴△ADE∽△BEF.
(2)解:∵DF与⊙O相切于点G,
∴OG⊥DG.
∴∠DGO=90°.
∵DH=OH=OG,
∴sin∠ODG=
=
.
∴∠ODG=30°.
∴∠GOE=120°.
∴S扇形OEG=
=3π.
在Rt△DGO中,
cos∠ODG=
=
=
.
∴DG=3
.
在Rt△DEF中,
tan∠EDF=
=
=
.
∴EF=3
.
∴S△DEF=
DE•EF=
×9×3
=
,
S△DGO=
DG•GO=
×3
×3=
.
∴S阴影=S△DEF-S△DGO-S扇形OEG
=
-
-3π
=.9
-3π
≈9×1.73-3×3.14
=6.15
≈6.2
∴图中阴影部分的面积约为6.2.
∴∠A=∠B=90°.
∵EF⊥DE,
∴∠DEF=90°.
∴∠AED=90°-∠BEF=∠EFB.
∵∠A=∠B,∠AED=∠EFB,
∴△ADE∽△BEF.
(2)解:∵DF与⊙O相切于点G,

∴OG⊥DG.
∴∠DGO=90°.
∵DH=OH=OG,
∴sin∠ODG=
| OG |
| OD |
| 1 |
| 2 |
∴∠ODG=30°.
∴∠GOE=120°.
∴S扇形OEG=
| 120π×32 |
| 360 |
在Rt△DGO中,
cos∠ODG=
| DG |
| DO |
| DG |
| 6 |
| ||
| 2 |
∴DG=3
| 3 |
在Rt△DEF中,
tan∠EDF=
| EF |
| DE |
| EF |
| 9 |
| ||
| 3 |
∴EF=3
| 3 |
∴S△DEF=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
27
| ||
| 2 |
S△DGO=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
9
| ||
| 2 |
∴S阴影=S△DEF-S△DGO-S扇形OEG
=
27
| ||
| 2 |
9
| ||
| 2 |
=.9
| 3 |
≈9×1.73-3×3.14
=6.15
≈6.2
∴图中阴影部分的面积约为6.2.
点评:本题考查了矩形的性质、相似三角形的判定、切线的性质、特殊角的三角函数值、扇形的面积等知识,考查了用割补法求不规则图形的面积.

练习册系列答案
相关题目
| 1 |
| 64 |
A、±
| ||
B、
| ||
C、±
| ||
D、
|
已知∠1与∠2互补,∠2与∠3互补,那么∠1与∠3的关系是( )
| A、相等 | B、互补 |
| C、互余 | D、不能确定 |
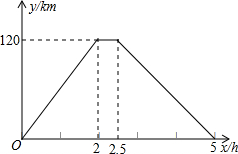 在一次运输任务中,一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返回.设汽车从甲地出发x(h)时,汽车与甲地的距离为y(km),y与x的函数关系如图所示.根据图象信息回答下列问题:
在一次运输任务中,一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返回.设汽车从甲地出发x(h)时,汽车与甲地的距离为y(km),y与x的函数关系如图所示.根据图象信息回答下列问题: