题目内容
10.分解因式(1)x3-6x2+9x;
(2)a2(x-y)+4(y-x).
分析 (1)原式提取x,再利用完全平方公式分解即可;
(2)原式变形后,提取公因式,再利用平方差公式分解即可.
解答 解:(1)原式=x(x2-6x+9)=x(x-3)2;
(2)原式=a2(x-y)-4(x-y)=(x-y)(a2-4)=(x-y)(a+2)(a-2).
点评 此题考查了因式分解-分组分解法,以及提公因式法,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
12.下列一元二次方程有两个相等的实数根的是( )
| A. | x2+1=0 | B. | x2+4x+4=0 | C. | x2+x+(-$\frac{1}{2}$)=0 | D. | x2-x+$\frac{1}{2}$=0 |
18.下列式子中,错误的是( )
| A. | $\sqrt{2}$×$\sqrt{8}$=4 | B. | $\sqrt{(-4)×(-9)}$=$\sqrt{-4}$×$\sqrt{-9}$ | C. | $\sqrt{\frac{4}{3}}$=$\frac{2}{3}$$\sqrt{3}$ | D. | $\frac{4\sqrt{18}}{2\sqrt{6}}$=2$\sqrt{3}$ |
5. 如图,四边形ABCD是正方形,点E在BC上,△ABE绕正方形的中心经顺时针旋转后与△DAF重合,则旋转角度是( )
如图,四边形ABCD是正方形,点E在BC上,△ABE绕正方形的中心经顺时针旋转后与△DAF重合,则旋转角度是( )
 如图,四边形ABCD是正方形,点E在BC上,△ABE绕正方形的中心经顺时针旋转后与△DAF重合,则旋转角度是( )
如图,四边形ABCD是正方形,点E在BC上,△ABE绕正方形的中心经顺时针旋转后与△DAF重合,则旋转角度是( )| A. | 120° | B. | 90° | C. | 60° | D. | 45° |
15.若M(-2,y1),N(-1,y2),P(2,y3)三点都在函数y=$\frac{k}{x}$(k<0)的图象上,则y1,y2,y3的大小关系是( )
| A. | y3>y1>y2 | B. | y3>y2>y1 | C. | y1>y2>y3 | D. | y2>y1>y3 |
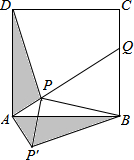 如图,点P是正方形ABCD内一点,PA=1,PB=2$\sqrt{2}$,PD=$\sqrt{10}$,将△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q.
如图,点P是正方形ABCD内一点,PA=1,PB=2$\sqrt{2}$,PD=$\sqrt{10}$,将△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q. 如图,A,B是4×4网格上的两个格点,在格点中任意放置点C,与点A,点B恰好围成等腰三角形的概率是$\frac{9}{25}$.
如图,A,B是4×4网格上的两个格点,在格点中任意放置点C,与点A,点B恰好围成等腰三角形的概率是$\frac{9}{25}$.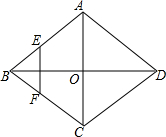 如图,菱形ABCD的对角线AC,BD相交于O点,E,F分别是AB,BC边上的中点,连接EF,若EF=$\sqrt{3}$,BD=4,则菱形ABCD的面积为4$\sqrt{3}$.
如图,菱形ABCD的对角线AC,BD相交于O点,E,F分别是AB,BC边上的中点,连接EF,若EF=$\sqrt{3}$,BD=4,则菱形ABCD的面积为4$\sqrt{3}$.