题目内容
1.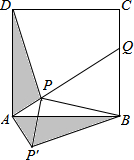 如图,点P是正方形ABCD内一点,PA=1,PB=2$\sqrt{2}$,PD=$\sqrt{10}$,将△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q.
如图,点P是正方形ABCD内一点,PA=1,PB=2$\sqrt{2}$,PD=$\sqrt{10}$,将△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q.(1)求PP′的长;
(2)求∠BPQ的大小.
分析 (1)根据正方形的性质得AB=AD,∠BAD=90°,再利用旋转的性质得AP=AP′,∠PAP′=∠DAB=90°,于是可判断△APP′是等腰直角三角形,根据等腰直角三角形的性质得PP′=$\sqrt{2}$PA=$\sqrt{2}$;
(2)由等腰直角三角形性质知∠APP′=45°,利用旋转的性质得PD=P′B=$\sqrt{10}$,接着根据勾股定理的逆定理可证明△PP′B为直角三角形,∠P′PB=90°,然后利用平角定义计算∠BPQ的度数.
解答 解:(1)∵四边形ABCD为正方形,
∴AB=AD,∠BAD=90°,
∵△ADP沿点A旋转至△ABP′,
∴AP=AP′=1,PD=P′B=$\sqrt{10}$,∠PAP′=∠DAB=90°,
∴△APP′是等腰直角三角形,
∴PP′=$\sqrt{P{A}^{2}+P′{A}^{2}}$=$\sqrt{2}$;
(2)∵△APP′是等腰直角三角形,
∴∠APP′=45°,
在△PP′B中,PP′=$\sqrt{2}$,PB=2$\sqrt{2}$,P′B=$\sqrt{10}$,
∵($\sqrt{2}$)2+(2$\sqrt{2}$)2=($\sqrt{10}$)2,
∴PP′2+PB2=P′B2,
∴△PP′B为直角三角形,∠P′PB=90°,
∴∠BPQ=180°-∠APP′-∠P′PB=180°-45°-90°=45°.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了正方形的性质和勾股定理的逆定理.

练习册系列答案
相关题目
3.对于某个一次函数,当x的值减小1个单位,y的值增加2个单位,则当x的值增加2个单位时,y的值将( )
| A. | 增加4个单位 | B. | 减小4个单位 | C. | 增加2个单位 | D. | 减小2个单位 |
16. 如图,△ABC绕点O顺时针旋转后,顶点A旋转到了点A′的位置,下列说法中,错误的是( )
如图,△ABC绕点O顺时针旋转后,顶点A旋转到了点A′的位置,下列说法中,错误的是( )
 如图,△ABC绕点O顺时针旋转后,顶点A旋转到了点A′的位置,下列说法中,错误的是( )
如图,△ABC绕点O顺时针旋转后,顶点A旋转到了点A′的位置,下列说法中,错误的是( )| A. | OA=OA′ | |
| B. | ∠AOA′是旋转角 | |
| C. | 作∠BOB′=∠AOA′,且OB′=OB,即可确定点B的对应点B′的位置 | |
| D. | 若点C的对应点为C′,则∠COC′=∠AOA′ |
 如图,在△ABC中,AB=AC,∠B=70°,将△ABC绕点C顺时针旋转α(其中0°<α<70°)后得到△A′B′C,连接AA′,则∠AA′B′=50°-$\frac{1}{2}$α(用含α的式子表示).
如图,在△ABC中,AB=AC,∠B=70°,将△ABC绕点C顺时针旋转α(其中0°<α<70°)后得到△A′B′C,连接AA′,则∠AA′B′=50°-$\frac{1}{2}$α(用含α的式子表示). 如图,在直角坐标系中,已知点B(0,6),O(0,0),D(8,0)和点C都在⊙A上,则sin∠BCO=$\frac{3}{5}$.
如图,在直角坐标系中,已知点B(0,6),O(0,0),D(8,0)和点C都在⊙A上,则sin∠BCO=$\frac{3}{5}$.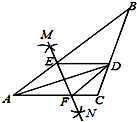 如图,在△ABC中,AD平分∠BAC,按如下步骤作图:第一步,分别以点A、D为圆心,以大于AD的一半长为半径在AD两侧作弧,交于两点M、N;第二步,连接MN分别交AB、AC于点E、F;第三步,连接DE、DF,则可以得到四边形AEDF的形状( )
如图,在△ABC中,AD平分∠BAC,按如下步骤作图:第一步,分别以点A、D为圆心,以大于AD的一半长为半径在AD两侧作弧,交于两点M、N;第二步,连接MN分别交AB、AC于点E、F;第三步,连接DE、DF,则可以得到四边形AEDF的形状( )