题目内容
20.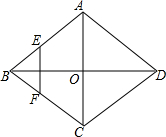 如图,菱形ABCD的对角线AC,BD相交于O点,E,F分别是AB,BC边上的中点,连接EF,若EF=$\sqrt{3}$,BD=4,则菱形ABCD的面积为4$\sqrt{3}$.
如图,菱形ABCD的对角线AC,BD相交于O点,E,F分别是AB,BC边上的中点,连接EF,若EF=$\sqrt{3}$,BD=4,则菱形ABCD的面积为4$\sqrt{3}$.
分析 根据EF是△ABC的中位线,根据三角形中位线定理求的AC的长,然后根据菱形的面积公式求解.
解答 解:∵E、F是AB和BC的中点,即EF是△ABC的中位线,
∴AC=2EF=2$\sqrt{3}$,
则S菱形ABCD=$\frac{1}{2}$AC•BD=$\frac{1}{2}$×2$\sqrt{3}$×4=4$\sqrt{3}$.
故答案是:4$\sqrt{3}$.
点评 本题考查了三角形的中位线定理和菱形的面积公式,理解中位线定理求的AC的长是关键.

练习册系列答案
相关题目
11.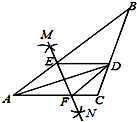 如图,在△ABC中,AD平分∠BAC,按如下步骤作图:第一步,分别以点A、D为圆心,以大于AD的一半长为半径在AD两侧作弧,交于两点M、N;第二步,连接MN分别交AB、AC于点E、F;第三步,连接DE、DF,则可以得到四边形AEDF的形状( )
如图,在△ABC中,AD平分∠BAC,按如下步骤作图:第一步,分别以点A、D为圆心,以大于AD的一半长为半径在AD两侧作弧,交于两点M、N;第二步,连接MN分别交AB、AC于点E、F;第三步,连接DE、DF,则可以得到四边形AEDF的形状( )
 如图,在△ABC中,AD平分∠BAC,按如下步骤作图:第一步,分别以点A、D为圆心,以大于AD的一半长为半径在AD两侧作弧,交于两点M、N;第二步,连接MN分别交AB、AC于点E、F;第三步,连接DE、DF,则可以得到四边形AEDF的形状( )
如图,在△ABC中,AD平分∠BAC,按如下步骤作图:第一步,分别以点A、D为圆心,以大于AD的一半长为半径在AD两侧作弧,交于两点M、N;第二步,连接MN分别交AB、AC于点E、F;第三步,连接DE、DF,则可以得到四边形AEDF的形状( )| A. | 仅仅只是平行四边形 | B. | 是矩形 | ||
| C. | 是菱形 | D. | 无法判断 |
5.下列选项中正确的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | $\frac{2x{y}^{2}}{4{x}^{2}y}$=$\frac{1}{2}$ | C. | $\frac{n}{m}$=$\frac{n-a}{m-a}$ | D. | 若a>0,则$\sqrt{a^2}=a$ |
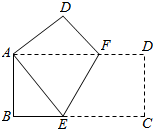 如图,将一个边长分别为4cm、8cm的矩形纸片ABCD折叠,使C点与A点重合,则EB的长是3cm.
如图,将一个边长分别为4cm、8cm的矩形纸片ABCD折叠,使C点与A点重合,则EB的长是3cm.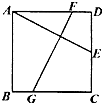 如图,已知正方形ABCD的边长为2,点E为CD的中点,点F、G分别在AD、BC上,FG⊥AE,则FG的长为$\sqrt{5}$.
如图,已知正方形ABCD的边长为2,点E为CD的中点,点F、G分别在AD、BC上,FG⊥AE,则FG的长为$\sqrt{5}$.