题目内容
5. 如图,四边形ABCD是正方形,点E在BC上,△ABE绕正方形的中心经顺时针旋转后与△DAF重合,则旋转角度是( )
如图,四边形ABCD是正方形,点E在BC上,△ABE绕正方形的中心经顺时针旋转后与△DAF重合,则旋转角度是( )| A. | 120° | B. | 90° | C. | 60° | D. | 45° |
分析 根据旋转性质得出旋转后A到D,只要根据正方形的性质和三角形的内角和定理求出∠AOD即可.
解答 解:如图所示: 将△ABE绕正方形的中心O按顺时针方向旋转到△DAF时,A和D重合,
将△ABE绕正方形的中心O按顺时针方向旋转到△DAF时,A和D重合,
即∠AOD是旋转角,
∵四边形ABCD是正方形,
∴∠DAO=∠ADO=45°,
∴∠AOD=180°-45°-45°=90°,
即旋转角是90°,
故选B.
点评 本题考查了旋转的性质和正方形性质,主要考查学生的理解能力和推理能力,关键是找到旋转角.

练习册系列答案
相关题目
7.下列图形中,是中心对称图形但不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
16. 如图,△ABC绕点O顺时针旋转后,顶点A旋转到了点A′的位置,下列说法中,错误的是( )
如图,△ABC绕点O顺时针旋转后,顶点A旋转到了点A′的位置,下列说法中,错误的是( )
 如图,△ABC绕点O顺时针旋转后,顶点A旋转到了点A′的位置,下列说法中,错误的是( )
如图,△ABC绕点O顺时针旋转后,顶点A旋转到了点A′的位置,下列说法中,错误的是( )| A. | OA=OA′ | |
| B. | ∠AOA′是旋转角 | |
| C. | 作∠BOB′=∠AOA′,且OB′=OB,即可确定点B的对应点B′的位置 | |
| D. | 若点C的对应点为C′,则∠COC′=∠AOA′ |
20.在Rt△ABC中,∠C=90°,AB=10,BC=6,则AC的长是( )
| A. | 8 | B. | 4$\sqrt{34}$ | C. | 64 | D. | 16 |
 如图,在直角坐标系中,已知点B(0,6),O(0,0),D(8,0)和点C都在⊙A上,则sin∠BCO=$\frac{3}{5}$.
如图,在直角坐标系中,已知点B(0,6),O(0,0),D(8,0)和点C都在⊙A上,则sin∠BCO=$\frac{3}{5}$.
 如图,点A在y=$\frac{1}{x}$双曲线上,点B在y=$\frac{3}{x}$双曲线上,且AB∥x轴,C、D在x轴上,若四边形ABCD为矩形,则它的面积为2.
如图,点A在y=$\frac{1}{x}$双曲线上,点B在y=$\frac{3}{x}$双曲线上,且AB∥x轴,C、D在x轴上,若四边形ABCD为矩形,则它的面积为2.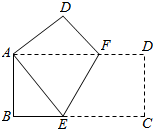 如图,将一个边长分别为4cm、8cm的矩形纸片ABCD折叠,使C点与A点重合,则EB的长是3cm.
如图,将一个边长分别为4cm、8cm的矩形纸片ABCD折叠,使C点与A点重合,则EB的长是3cm.