题目内容
15.若M(-2,y1),N(-1,y2),P(2,y3)三点都在函数y=$\frac{k}{x}$(k<0)的图象上,则y1,y2,y3的大小关系是( )| A. | y3>y1>y2 | B. | y3>y2>y1 | C. | y1>y2>y3 | D. | y2>y1>y3 |
分析 先根据k<0判断出函数图象所在的象限及其增减性,再根据各点横坐标的大小即可得出结论.
解答 解:∵函数y=$\frac{k}{x}$中k<0,
∴函数图象的两个分支分别位于二四象限,且在每一象限内y随x的增大而增大.
∵-2<-1<0,c>0,
∴点M、N在第二象限,点P在第四象限,
∴y2>y1>y3.
故选D.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
17. 如图是一个零件的立体图,该零件的俯视图是( )
如图是一个零件的立体图,该零件的俯视图是( )
 如图是一个零件的立体图,该零件的俯视图是( )
如图是一个零件的立体图,该零件的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
5.下列选项中正确的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | $\frac{2x{y}^{2}}{4{x}^{2}y}$=$\frac{1}{2}$ | C. | $\frac{n}{m}$=$\frac{n-a}{m-a}$ | D. | 若a>0,则$\sqrt{a^2}=a$ |
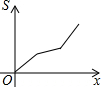
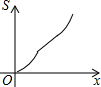
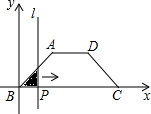 如图,在四边形ABCD中,AD∥BC,AB=DC,以点B为原点,BC边所在的直线为x轴建立平面直角坐标系,直线l与y轴重合且向右平移,若其扫过的面积(阴影部分)为S,设向右平移的距离BP为x,则S关于x的函数图象大致是( )
如图,在四边形ABCD中,AD∥BC,AB=DC,以点B为原点,BC边所在的直线为x轴建立平面直角坐标系,直线l与y轴重合且向右平移,若其扫过的面积(阴影部分)为S,设向右平移的距离BP为x,则S关于x的函数图象大致是( )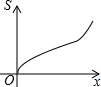

 已知二次函数y=2x2-x-3.
已知二次函数y=2x2-x-3.