题目内容
7.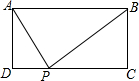 如图,矩形ABCD中,AB>AD,P为CD上异于C、D的一动点,且△APB为直角三角形,
如图,矩形ABCD中,AB>AD,P为CD上异于C、D的一动点,且△APB为直角三角形,(1)若AB=5,AD=2,则DP=1或4;
(2)若AB=a,AD=b,当a、b满足什么条件时,使△ABP为直角三角形的P点只有一个?
分析 (1)在矩形ABCD中,根据矩形的性质得到CD=AB=5,CB=AD=2,∠D=∠C=∠DAB=90°,于是推出∠DAP=∠BPC,得到△APD∽△PBC,证得$\frac{AD}{PC}=\frac{PD}{BC}$,即可求得结论;
(2)当△APB为等腰直角三角形时,即PA=PB时,使△ABP为直角三角形的P点只有一个,根据等腰直角三角形的性质得到∠PAB=∠PBA=45°,于是推出△ADP与△PBC是等腰直角三角形,于是得到CD=2AD,即a=2b时,使△ABP为直角三角形的P点只有一个.
解答 解:(1)在矩形ABCD中,
∵CD=AB=5,CB=AD=2,∠D=∠C=∠DAB=90°,
∵∠APB=90°,
∴∠DAP+∠DPA=∠DPA+∠BPC=90°,
∴∠DAP=∠BPC,
∴△APD∽△PBC,
∴$\frac{AD}{PC}=\frac{PD}{BC}$,
即$\frac{2}{5-PD}=\frac{PD}{2}$,
解得:PD=1,或PD=4;
故答案为:1或4;
(2)当△APB为等腰直角三角形时,
即PA=PB时,使△ABP为直角三角形的P点只有一个,
∴∠PAB=∠PBA=45°,
∴∠DAP=∠PBC=45°,
∴△ADP与△PBC是等腰直角三角形,
∴CD=2AD,
即a=2b时,使△ABP为直角三角形的P点只有一个.
点评 本题考查了相似三角形2,等腰直角三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
 如图,A点表示数a,B点表示数b,在a+b,b-a,ab,a+b+3中正数是b-a,a+b+3.
如图,A点表示数a,B点表示数b,在a+b,b-a,ab,a+b+3中正数是b-a,a+b+3.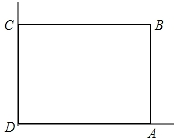 在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.
在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm. 如图,在边长为2的正方形ABCD中,P为BC边上的任意一点(点P与B,C不重合),且DQ⊥AP,垂足为Q.设AP=x.DQ=y.
如图,在边长为2的正方形ABCD中,P为BC边上的任意一点(点P与B,C不重合),且DQ⊥AP,垂足为Q.设AP=x.DQ=y. 如图,在直角梯形ABCD中,∠D=∠C=90°.若∠DAB的平分线AE交CD于E,连接BE,且BE恰好平分∠ABC.求证:AB=BC+AD.
如图,在直角梯形ABCD中,∠D=∠C=90°.若∠DAB的平分线AE交CD于E,连接BE,且BE恰好平分∠ABC.求证:AB=BC+AD.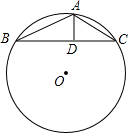 如图,△ABC内接于⊙O,AD垂直于BC,垂足为D,AD=2,CD=3,BD=4,则⊙O的直径为$\sqrt{65}$.
如图,△ABC内接于⊙O,AD垂直于BC,垂足为D,AD=2,CD=3,BD=4,则⊙O的直径为$\sqrt{65}$.