题目内容
2.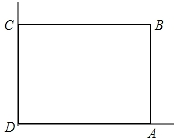 在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.
在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.(1)若花园的面积为192m2,求x的值;
(2)当AB的长为多少时,花园的面积最大,最大面积是多少?
分析 (1)根据题意得出长×宽=192列出方程,进一步解方程得出答案即可;
(2)设花园的面积为S,根据矩形的面积公式得到S=x(28-x)=-x2+28x=-(x-14)2+196,于是得到结果.
解答 解:(1)∵AB=xm,则BC=(28-x)m,
∴x(28-x)=192,
解得:x1=12,x2=16,
答:x的值为12m或16m;
(2)设花园的面积为S,
由题意得:S=x(28-x)=-x2+28x=-(x-14)2+196,
∵a=-1<0,
∴当x=14时,S最大,最大值为:196.
点评 此题主要考查了二次函数的应用以及二次函数最值求法,得出S与x的函数关系式是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.若关于x的一元二次方程x2+4x+a=0有两个不相等的实数根,则a的取值范围是( )
| A. | a<-4 | B. | a<4 | C. | a>-4 | D. | a>4 |
 画出下面立体图形的主视图、俯视图:
画出下面立体图形的主视图、俯视图: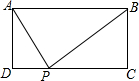 如图,矩形ABCD中,AB>AD,P为CD上异于C、D的一动点,且△APB为直角三角形,
如图,矩形ABCD中,AB>AD,P为CD上异于C、D的一动点,且△APB为直角三角形,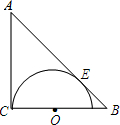 如图,在△ABC中,∠C=90°,AC=BC=2$\sqrt{2}$+2,在BC上取一点O,以O为圆心,OC为半径作半圆与AB相切于点E.求⊙O的半径.
如图,在△ABC中,∠C=90°,AC=BC=2$\sqrt{2}$+2,在BC上取一点O,以O为圆心,OC为半径作半圆与AB相切于点E.求⊙O的半径.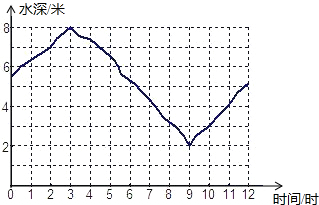 海水受日月的引力而产生潮汐现象,早晨海水上涨叫潮,黄昏海水上涨叫汐,合称潮汐,潮汐与人类的生活有着密切的联系,如图是某港口从0时到12时的水深情况.
海水受日月的引力而产生潮汐现象,早晨海水上涨叫潮,黄昏海水上涨叫汐,合称潮汐,潮汐与人类的生活有着密切的联系,如图是某港口从0时到12时的水深情况.