题目内容
17.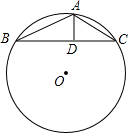 如图,△ABC内接于⊙O,AD垂直于BC,垂足为D,AD=2,CD=3,BD=4,则⊙O的直径为$\sqrt{65}$.
如图,△ABC内接于⊙O,AD垂直于BC,垂足为D,AD=2,CD=3,BD=4,则⊙O的直径为$\sqrt{65}$.
分析 连接AO并延长交⊙O于E,连接BE,于是得到∠E=∠C,∠ABE=90°,根据勾股定理得到AC=$\sqrt{A{D}^{2}+C{D}^{2}}$=$\sqrt{13}$,AB=$\sqrt{A{D}^{2}+B{D}^{2}}$=2$\sqrt{5}$,通过△ABE∽△ADC,得到$\frac{AE}{AC}=\frac{AB}{AD}$,于是求得AE=$\sqrt{65}$,即可得到答案.
解答 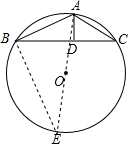 解:连接AO并延长交⊙O于E,连接BE,
解:连接AO并延长交⊙O于E,连接BE,
∴∠E=∠C,∠ABE=90°,
∵AD⊥BC,
∴∠ADC=∠ADB=90°,
∵AD=2,CD=3,BD=4,
∴AC=$\sqrt{A{D}^{2}+C{D}^{2}}$=$\sqrt{13}$,AB=$\sqrt{A{D}^{2}+B{D}^{2}}$=2$\sqrt{5}$,
∵∠ABE=∠ADC=90°,
∴△ABE∽△ADC,
∴$\frac{AE}{AC}=\frac{AB}{AD}$,
即:$\frac{AE}{\sqrt{13}}=\frac{2\sqrt{5}}{2}$,
∴AE=$\sqrt{65}$,
∴⊙O的直径为$\sqrt{65}$.
故答案为:$\sqrt{65}$.
点评 本题考查了相似三角形的判定和性质,勾股定理,圆周角定理,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
9.下列判断中,正确的是( )
| A. | 平方等于它本身的有理数是1,或-1,或0 | |
| B. | 倒数等于它本身的有理数是1,或-1,或0 | |
| C. | 平方等于9的有理数是3和-3 | |
| D. | $\frac{355}{113}$是圆周率的近似值,因此$\frac{355}{113}$是无理数 |
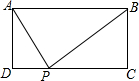 如图,矩形ABCD中,AB>AD,P为CD上异于C、D的一动点,且△APB为直角三角形,
如图,矩形ABCD中,AB>AD,P为CD上异于C、D的一动点,且△APB为直角三角形,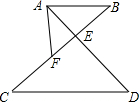 如图所示,已知AB∥CD,AD,BC相交于E,F为EC上一点,且∠EAF=∠C.
如图所示,已知AB∥CD,AD,BC相交于E,F为EC上一点,且∠EAF=∠C.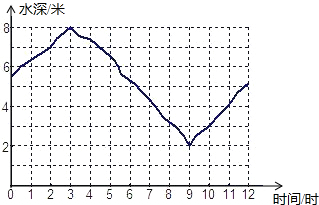 海水受日月的引力而产生潮汐现象,早晨海水上涨叫潮,黄昏海水上涨叫汐,合称潮汐,潮汐与人类的生活有着密切的联系,如图是某港口从0时到12时的水深情况.
海水受日月的引力而产生潮汐现象,早晨海水上涨叫潮,黄昏海水上涨叫汐,合称潮汐,潮汐与人类的生活有着密切的联系,如图是某港口从0时到12时的水深情况.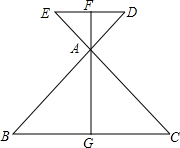 如图所示,BD与CE相交于点A,且AB=AC,AD=AE,△ABC的中线AG的反向延长线交DE于点F,则AF与DE垂直吗?用“三线合一”的方法说明理由.
如图所示,BD与CE相交于点A,且AB=AC,AD=AE,△ABC的中线AG的反向延长线交DE于点F,则AF与DE垂直吗?用“三线合一”的方法说明理由.