题目内容
19. 如图,在边长为2的正方形ABCD中,P为BC边上的任意一点(点P与B,C不重合),且DQ⊥AP,垂足为Q.设AP=x.DQ=y.
如图,在边长为2的正方形ABCD中,P为BC边上的任意一点(点P与B,C不重合),且DQ⊥AP,垂足为Q.设AP=x.DQ=y.(1)如果连接DP,那么△ADP的面积等于$\frac{1}{2}$xy;
(2)当点P为BC上的一个动点时,线段DQ也随之变化,若$\frac{AP}{AD}$=$\frac{AB}{DQ}$,求y与x之间的函数关系式,并指出x的取值范围.
分析 (1)根据三角形的面积公式即可求得结论;
(2)根据四边形ABCD是正方形,得AD∥BC,∠B=90°,∠DAP=∠APB,根据DQ⊥AP,得∠B=∠AQD,即可证出△DAQ∽△APB;
根据△DAQ∽△APB,得$\frac{DQ}{AB}=\frac{DA}{AP}$,再把AB=2,DA=2,PA=x,DQ=y代入得出$\frac{y}{2}=\frac{2}{x}$,y=$\frac{4}{x}$.根据点P在BC上移到C点时,PA最长,求出此时PA的长即可得出x的取值范围.
解答 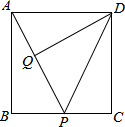 解:(1)∵DQ⊥AP,垂足为Q,设AP=x,DQ=y,
解:(1)∵DQ⊥AP,垂足为Q,设AP=x,DQ=y,
∴S△ADP=$\frac{1}{2}$AP•DQ=$\frac{1}{2}$xy;
故答案为:$\frac{1}{2}$xy;
(2)∵四边形ABCD是正方形,
∴AD∥BC,∠B=90°,
∴∠DAP=∠APB,
∵DQ⊥AP,
∴∠AQD=90°,
∴∠B=∠AQD,
∴△DAQ∽△APB;
∴$\frac{DQ}{AB}=\frac{DA}{AP}$,
∵AB=2,
∴DA=2,
∵PA=x,DQ=y,
∴$\frac{y}{2}=\frac{2}{x}$,
∴y=$\frac{4}{x}$.
∵点P在BC上移到C点时,PA最长,此时PA=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
又∵P是BC边上与B、C不重合的任意一点,
∴x的取值范围是;2<x<2$\sqrt{2}$.
点评 此题考查了相似三角形的判定与性质,用到的知识点是相似三角形的判定与性质、正方形的性质,关键是能根据两三角形相似求出函数关系式.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
11.若关于x的一元二次方程x2+4x+a=0有两个不相等的实数根,则a的取值范围是( )
| A. | a<-4 | B. | a<4 | C. | a>-4 | D. | a>4 |
9.下列判断中,正确的是( )
| A. | 平方等于它本身的有理数是1,或-1,或0 | |
| B. | 倒数等于它本身的有理数是1,或-1,或0 | |
| C. | 平方等于9的有理数是3和-3 | |
| D. | $\frac{355}{113}$是圆周率的近似值,因此$\frac{355}{113}$是无理数 |
 画出下面立体图形的主视图、俯视图:
画出下面立体图形的主视图、俯视图: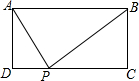 如图,矩形ABCD中,AB>AD,P为CD上异于C、D的一动点,且△APB为直角三角形,
如图,矩形ABCD中,AB>AD,P为CD上异于C、D的一动点,且△APB为直角三角形,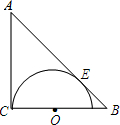 如图,在△ABC中,∠C=90°,AC=BC=2$\sqrt{2}$+2,在BC上取一点O,以O为圆心,OC为半径作半圆与AB相切于点E.求⊙O的半径.
如图,在△ABC中,∠C=90°,AC=BC=2$\sqrt{2}$+2,在BC上取一点O,以O为圆心,OC为半径作半圆与AB相切于点E.求⊙O的半径. 如图,AB=AC,BD=CD.
如图,AB=AC,BD=CD.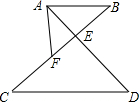 如图所示,已知AB∥CD,AD,BC相交于E,F为EC上一点,且∠EAF=∠C.
如图所示,已知AB∥CD,AD,BC相交于E,F为EC上一点,且∠EAF=∠C.