题目内容
8.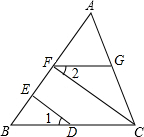 如图所示,∠1=∠2,CF⊥AB,DE⊥AB,垂足分别为点F、E,求证:FG∥BC.
如图所示,∠1=∠2,CF⊥AB,DE⊥AB,垂足分别为点F、E,求证:FG∥BC.证明:∵CF⊥AB、DE⊥AB(已知)
∴∠BED=90°、∠BFC=90°
∴∠BED=∠BFC
∴(ED)∥(FC)
(同位角相等,两直线平行)
∴∠1=∠BCF(两直线平行,同位角相等)
又∵∠1=∠2(已知)
∴∠2=∠BCF(等量代换)
∴FG∥BC(内错角相等,两直线平行)
分析 根据垂直定义求出∠BED=∠BFC,根据平行线的判定得出ED∥FC,根据平行线的性质得出∠1=∠BCF,求出∠2=∠BCF,根据平行线的判定推出即可.
解答 证明:∵CF⊥AB、DE⊥AB(已知),
∴∠BED=90°,∠BFG=90°,
∴∠BED=∠BFC,
∴(ED)∥(FC)(同位角相等,两直线平行),
∴∠1=∠BCF(两直线平行,同位角相等),
∵∠1=∠2,
∴∠2=∠BCF(等量代换),
∴FG∥BC(内错角相等,两直线平行),
故答案为:ED,FC,同位角相等,两直线平行,两直线平行,同位角相等,等量代换,内错角相等,两直线平行.
点评 本题考查了平行线的判定和性质的应用,能运用平行线的判定和性质进行推理是解此题的关键,难度适中.

练习册系列答案
相关题目
3.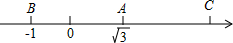 如图,数轴上A、B两点对应的实数是$\sqrt{3}$和-1,AC=AB,则点C所对应的实数是( )
如图,数轴上A、B两点对应的实数是$\sqrt{3}$和-1,AC=AB,则点C所对应的实数是( )
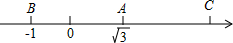 如图,数轴上A、B两点对应的实数是$\sqrt{3}$和-1,AC=AB,则点C所对应的实数是( )
如图,数轴上A、B两点对应的实数是$\sqrt{3}$和-1,AC=AB,则点C所对应的实数是( )| A. | 1+$\sqrt{3}$ | B. | 2+$\sqrt{3}$ | C. | 2$\sqrt{3}$-1 | D. | 2$\sqrt{3}$+1 |
20. 某工厂投入生产一种机器,当该机器生产数量至少10台,但不超过70台,每台成本y与生产数量x之间是一次函数关系,函数y与自变量x的部分对应值如表:
某工厂投入生产一种机器,当该机器生产数量至少10台,但不超过70台,每台成本y与生产数量x之间是一次函数关系,函数y与自变量x的部分对应值如表:
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
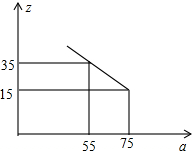
(2)市场调查发现,这种机器每月销售量z(台)与售价a(万元∕台)之间满足如图所示的函数关系,求z与a之间的函数关系式.
(3)若该厂第一个月生产这种机器50台,且第一个月按同一售价共卖出这种机器25台,请你求出该厂第一个月销售这种机器的利润.(注:利润=售价-成本)
 某工厂投入生产一种机器,当该机器生产数量至少10台,但不超过70台,每台成本y与生产数量x之间是一次函数关系,函数y与自变量x的部分对应值如表:
某工厂投入生产一种机器,当该机器生产数量至少10台,但不超过70台,每台成本y与生产数量x之间是一次函数关系,函数y与自变量x的部分对应值如表:| x(单位:台) | 10 | 20 | 30 |
| y(单位:万元∕台) | 60 | 55 | 50 |
(2)市场调查发现,这种机器每月销售量z(台)与售价a(万元∕台)之间满足如图所示的函数关系,求z与a之间的函数关系式.
(3)若该厂第一个月生产这种机器50台,且第一个月按同一售价共卖出这种机器25台,请你求出该厂第一个月销售这种机器的利润.(注:利润=售价-成本)
18.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图1,C地位于A,B两地之间,甲步行直接从C地前往B地;乙骑自行车由C地先回A地,再从A地前往B地(在A地停留时间忽略不计).已知两人同时出发且速度不变,乙的速度是甲的$\frac{5}{2}$倍,设出发xmin后甲、乙两人离C地的距离分别为y1m,y2m,图②中线段OM表示y1与x的函数图象.
如图1,C地位于A,B两地之间,甲步行直接从C地前往B地;乙骑自行车由C地先回A地,再从A地前往B地(在A地停留时间忽略不计).已知两人同时出发且速度不变,乙的速度是甲的$\frac{5}{2}$倍,设出发xmin后甲、乙两人离C地的距离分别为y1m,y2m,图②中线段OM表示y1与x的函数图象. 在平面直角坐标系中,O为坐标原点,A(-2,3),B(2,2).
在平面直角坐标系中,O为坐标原点,A(-2,3),B(2,2). 已知,如图,直线AB与CD相交于点O,OE平分∠AOC,若∠EOC=25°,则∠BOD的度数为50°.
已知,如图,直线AB与CD相交于点O,OE平分∠AOC,若∠EOC=25°,则∠BOD的度数为50°.