题目内容
13.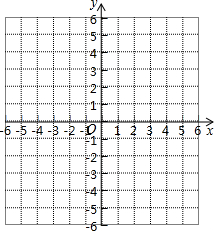 在平面直角坐标系中,O为坐标原点,A(-2,3),B(2,2).
在平面直角坐标系中,O为坐标原点,A(-2,3),B(2,2).(1)画出三角形OAB;
(2)求三角形OAB的面积;
(3)若三角形OAB中任意一点P(x1,y1)经平移后对应点为P1(x1+4,y1-3),请画出三角形OAB平移后得到的三角形O1A1B1,并写出点O1,A1,B${{\;}_{1}}_{\;}^{\;}$的坐标.
分析 (1)直接利用A,B点坐标,在坐标系中标出得出答案;
(2)直接利用三角形面积求法得出答案;
(3)直接利用平移的性质得出对应点位置进而得出答案.
解答  解:(1)如图所示:△OAB即为所求;
解:(1)如图所示:△OAB即为所求;
(2)S△OAB=12-$\frac{1}{2}$×1×4-$\frac{1}{2}$×2×3-$\frac{1}{2}$×2×2=5;
(3)如图所示:△O1A1B1,即为所求,O1(4,-3),A1 (2,0),B1 (6,-1).
点评 此题主要考查了平移变换以及三角形面积,正确得出对应点位置是解题关键.

练习册系列答案
相关题目
4.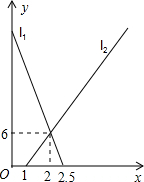 小南骑自行车从A地向B地出发,1小时后小通步行从B地向A地出发.如图,两条线段l1、l2分别表示小南、小通离B地的距离y(单位:km)与所用时间x(单位:h)之间的函数图象,根据图中的信息,则小南、小通的速度分别是( )
小南骑自行车从A地向B地出发,1小时后小通步行从B地向A地出发.如图,两条线段l1、l2分别表示小南、小通离B地的距离y(单位:km)与所用时间x(单位:h)之间的函数图象,根据图中的信息,则小南、小通的速度分别是( )
 小南骑自行车从A地向B地出发,1小时后小通步行从B地向A地出发.如图,两条线段l1、l2分别表示小南、小通离B地的距离y(单位:km)与所用时间x(单位:h)之间的函数图象,根据图中的信息,则小南、小通的速度分别是( )
小南骑自行车从A地向B地出发,1小时后小通步行从B地向A地出发.如图,两条线段l1、l2分别表示小南、小通离B地的距离y(单位:km)与所用时间x(单位:h)之间的函数图象,根据图中的信息,则小南、小通的速度分别是( )| A. | 12 km/h,3 km/h | B. | 15km/h,3km/h | C. | 12 km/h,6 km/h | D. | 15km/h,6km/h |
18.某班同学在探究弹簧长度跟外力的关系变化时,实验记录得到的数据如表:
则y关于x的函数图象是( )
| 砝码的质量(x克) | 0 | 50 | 100 | 150 | 200 | 250 | 300 | 400 | 500 |
| 指针位置(y厘米) | 2 | 3 | 4 | 5 | 6 | 7 | 7.5 | 7.5 | 7.5 |
| A. | 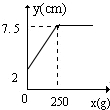 | B. | 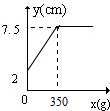 | C. | 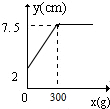 | D. |  |
3.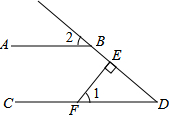 如图,AB∥CD,FE⊥DB,垂足为E,∠1=50°,则∠2的度数是( )
如图,AB∥CD,FE⊥DB,垂足为E,∠1=50°,则∠2的度数是( )
 如图,AB∥CD,FE⊥DB,垂足为E,∠1=50°,则∠2的度数是( )
如图,AB∥CD,FE⊥DB,垂足为E,∠1=50°,则∠2的度数是( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
 如图所示,∠AOB=30°,∠BOC=40°,∠COD=26°,OE平分∠AOD,求∠BOE的度数.
如图所示,∠AOB=30°,∠BOC=40°,∠COD=26°,OE平分∠AOD,求∠BOE的度数.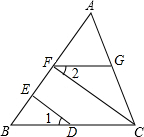 如图所示,∠1=∠2,CF⊥AB,DE⊥AB,垂足分别为点F、E,求证:FG∥BC.
如图所示,∠1=∠2,CF⊥AB,DE⊥AB,垂足分别为点F、E,求证:FG∥BC.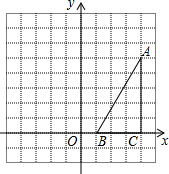 如图,在方格纸中(小正方形的边长为1),△ABC的三个顶点均为格点,将△ABC沿x轴向左平移5个单位长度,根据所给的直角坐标系(O是坐标原点),解答下列问题:①画出平移后的△A′B′C′.②直接写出点A′、B′、C′的坐标.
如图,在方格纸中(小正方形的边长为1),△ABC的三个顶点均为格点,将△ABC沿x轴向左平移5个单位长度,根据所给的直角坐标系(O是坐标原点),解答下列问题:①画出平移后的△A′B′C′.②直接写出点A′、B′、C′的坐标.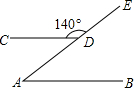 如图,点D在射线AE上,AB∥CD,∠CDE=140°,求∠A的度数.
如图,点D在射线AE上,AB∥CD,∠CDE=140°,求∠A的度数.