题目内容
13. 如图,矩形ABCD中,AC、BD交于O点,AE平分∠BAD交BC于E点且∠AOD=120°,求∠AOE的度数.
如图,矩形ABCD中,AC、BD交于O点,AE平分∠BAD交BC于E点且∠AOD=120°,求∠AOE的度数.
分析 由矩形ABCD,得到OA=OB,根据AE平分∠BAD,得到等边三角形OAB,推出AB=OB,求出∠OAB、∠OBC的度数,根据平行线的性质和等角对等边得到OB=BE,根据三角形的内角和定理即可求出答案.
解答 解:∵四边形ABCD是矩形,
∴AD∥BC,AC=BD,OA=OC,OB=OD,∠BAD=90°,
∴OA=OB,∠DAE=∠AEB,
∵AE平分∠BAD,
∴∠BAE=∠DAE=45°=∠AEB,
∴AB=BE,
∵∠CAE=15°,
∴∠DAC=45°-15°=30°,
∠BAC=60°,
∴△BAO是等边三角形,
∴AB=OB,∠ABO=60°,
∴∠OBC=90°-60°=30°,
∵AB=OB=BE,
∴∠BOE=∠BEO=$\frac{1}{2}$(180°-30°)=75°,
∴∠AOE=60°+75°=135°.
点评 本题主要考查了三角形的内角和定理,矩形的性质,等边三角形的性质和判定,平行线的性质,角平分线的性质,等腰三角形的判定等知识点,解此题的关键是求出∠OBC的度数和求OB=BE.

练习册系列答案
相关题目
3.下列哪个条件不能判定两直线平行( )
| A. | 同位角相等 | B. | 对顶角相等 | C. | 内错角相等 | D. | 同旁内角互补 |
4.小明和3个女生、4个男生玩丢手绢的游戏,如果小明随意将手绢丢在一名同学后面,那么这名同学不是女生的概率是( )
| A. | $\frac{3}{4}$ | B. | $\frac{3}{8}$ | C. | $\frac{4}{7}$ | D. | $\frac{3}{7}$ |
3.下列运算正确的是( )
| A. | b•b3=b4 | B. | x3+x3=x6 | C. | 4a3•2a2=8a6 | D. | 5a2-3a2=2 |

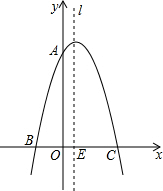 已知二次函数y=-x2+bx+c的图象与x轴交于B(-2,0),C(4,0)两点,点E是对称轴l与x轴的交点.
已知二次函数y=-x2+bx+c的图象与x轴交于B(-2,0),C(4,0)两点,点E是对称轴l与x轴的交点. 如图,△ABC以点O为旋转中心,旋转180°后得到△A′B′C′.ED是△ABC的中位线,经旋转后为线段E′D′.已知E′D′=2,则BC的值是( )
如图,△ABC以点O为旋转中心,旋转180°后得到△A′B′C′.ED是△ABC的中位线,经旋转后为线段E′D′.已知E′D′=2,则BC的值是( )