题目内容
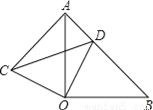
如图所示、△AOB和△COD均为等腰直角三角形，∠AOB=∠COD=90°，D在AB上．
（1）求证：△AOC≌△BOD；
（2）若AD=1，BD=2，求CD的长．
（1）证明见解析；（2）CD的长为．
【解析】（1）证明：如右图1，
，
又，
（2）由有： ， ，
，故
不等式的解集在数轴上表示如图所示，则该不等式可能是___________________.
不唯一，如x－1≤0
【解析】由图形可知，不等式的解集为x≤1.只要所写的不等式的解集为x≤1，即可，答案不唯一. 已知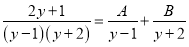
，求A、B的值．
A=1，B=1.
【解析】试题分析：已知等式右边两项通分并利用同分母分式的加法法则计算，利用分式相等的条件即可求出A与B．
试题解析：
【解析】
＝＝＝，
∴，
解得： ． 某地区林业局要考察一种树苗移植的成活率,对该地区这种树苗移植成活的情况进行调查统计,并绘制了如图所示的统计图,根据统计图提供的信息解决下列问题:
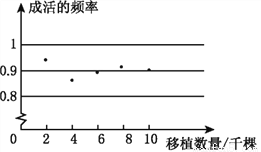
(1)这种树苗成活的频率稳定在___________,成活的概率估计值为___________.
(2)该地区已经移植这种树苗5万棵.
①估计这种树苗成活___________万棵.
②如果该地区计划成活18万棵这种树苗,那么还需移植这种树苗约多少万棵?
（1）0.9附近，0.9；（2）①4.5，15万棵.
【解析】（1）由图可知，成活概率在0.9上下波动，故可估计这种树苗成活的频率稳定在0.9，成活的概率估计值为0.9；
（2）①5×成活率即为所求的成活的树苗棵树；
②方法1:利用成活率求得需要树苗棵树，减去已移植树苗数即为所求的树苗的棵树；
方法2：设还需移植这种树苗万棵，根据成活率及成活总数列出方程即可。 动物学家通过大量的调查估计，某种动物活到20岁的概率为0.8，活到25岁的概率为0.6，则现年20岁的这种动物活到25岁的概率是（ ）
A. 0.8 B. 0.75 C. 0.6 D. 0.48
B
【解析】设共有这种动物x只，则活到20岁的只数为0.8x,活到25岁的只数为0.6x,故现年20岁到这种动物活到25岁的概率为=0.75,故选B. 下列命题中，其逆命题成立的是__．（只填写序号）
①同旁内角互补，两直线平行；
②如果两个角是直角，那么它们相等；
③如果两个实数相等，那么它们的平方相等；
④如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形是直角三角形．
①④
【解析】把一个命题的条件和结论互换就得到它的逆命题，再分析逆命题是否为真命题，需要分别分析各题设是否能推出结论，从而利用排除法得出答案。
①两直线平行，同旁内角互补，正确；
②如果两个角相等，那么它们是直角，错误；
③如果两个实数的平方相等，那么这两个实数相等，错误；
④如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形是直角三角形，正确．
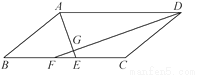
... 已知：如图，在?ABCD中，∠ADC，∠DAB的平分线DF，AE分别与线段BC相交于点F，E，DF与AE相交于点G．
（1）求证：AE⊥DF；
（2）若AD＝10，AB＝6，AE＝4，求DF的长．
（1）证明见解析；（2）．
【解析】试题分析：（1）根据平行四边形的性质和平行线的性质推出∠ADC+∠DAB=180°，根据角平分线得到∠ADF+∠DAE=（∠ADC+∠DAB）=90°，即可求出结论；
（2）过点D作DH∥AE，交BC的延长线于点H，得到平行四边形AEHD，求出DH=AE=4，EH=AD=10，根据平行四边形的性质和平行线的性质推出DC=FC，AB=EB，求出BF、F... 为了了解参加某运动会的2000名运动员的年龄情况，从中抽查了100名运动员的年龄，“某运动员被抽到”这一事件是______事件．
随机.
【解析】由题意知是从2000名运动员的年龄中抽取100名运动员的年龄，每一名运动员被投到的频率为，即为，所以某运动员被抽到这一事件是随机事件. 如图，等腰△ABC中，AB＝AC，∠DBC＝15°，AB的垂直平分线MN交AC于点D，则∠A的度数是________．
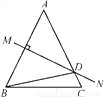
50°
【解析】根据线段垂直平分线上的点到两端点的距离相等可得AD=BD，根据等边对等角可得∠A=∠ABD，然后表示出∠ABC，再根据等腰三角形两底角相等可得∠C=∠ABC，然后根据三角形的内角和定理列出方程求解即可．
【解析】
∵MN是AB的垂直平分线，
∴AD=BD，
∴∠A=∠ABD，
∵∠DBC=15°，
∴∠ABC=∠A+15°，
∵AB=AC...