题目内容
已知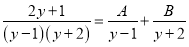
，求A、B的值．
A=1，B=1.
【解析】试题分析：已知等式右边两项通分并利用同分母分式的加法法则计算，利用分式相等的条件即可求出A与B．
试题解析：
【解析】
＝＝＝，
∴，
解得： ．
练习册系列答案
相关题目
如图，AC是□ABCD的一条对角线，BM⊥AC， DN⊥AC，垂足分别为M，N，四边形BMDN是平行四边形吗?请选择一种你认为比较好的方法证明．
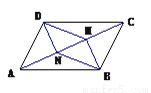
答案见解析
【解析】试题分析：由四边形ABCD是平行四边形，可得AD=BC，AD∥BC，又由BM⊥AC，DN⊥AC，即可得BM∥DN，∠DNA=∠BMC=90°，然后利用AAS证得△ADN≌△CBM，即可得DN=BM，由有一组对边相等且平行的四边形是平行四边形，即可证得四边形BMDN是平行四边形．
试题解析：【解析】
四边形BMDN是平行四边形．理由如下：
∵四边形ABCD是平... 如图，M，N两点在数轴上表示的数分别是m，n，则下列式子中成立的是（ ）
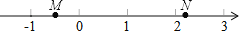
A. m+n＜0 B. 
m＜
n C. |m|
|n|＞0 D. 2+m＜2+n
D
【解析】试题分析：根据M、N两点在数轴上的位置判断出其取值范围，再对各选项进行逐一作出判断：
由M、N两点在数轴上的位置可知：-1＜M＜0，N＞2，
∵-1＜M＜0，N＞2，∴M+N＞0，故A错误.
∵M＜N，∴-M＞-N，故B错误.
∵-1＜M＜0，N＞2，∴|m|-|n|＜0，故C错误．
∵M＜N，∴2+m＜2+n，故D正确.
故选D． 命题“全等三角形的面积相等”的逆命题是 ．
面积相等的两个三角形全等
【解析】试题分析：把一个命题的题设和结论互换就可得到它的逆命题： “全等三角形的面积相等”的逆命题是：面积相等的三角形是全等三角形． 如图，在△ABC中，AB=AC，BD平分∠ABC交AC于点D，AE∥BD交CB的延长线于点E．若∠E=35°，则∠BAC的度数为（ ）
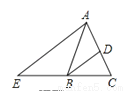
A. 40° B. 45° C. 60° D. 70°
A
【解析】根据平行线的性质可得∠CBD的度数，根据角平分线的性质可得∠CBA的度数，根据等腰三角形的性质可得∠C的度数，根据三角形内角和定理可得∠BAC的度数．
【解析】
∵AE∥BD，∴∠CBD=∠E=35°，∵BD平分∠ABC，∴∠CBA=70°，∵AB=AC，
∴∠C=∠CBA=70°，∴∠BAC=180°﹣70°×2=40°．
故选A．
“点睛”考查了平行... 如果分式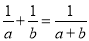
，那么
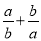的值( )
A. 1 B. －1 C. 2 D. －2
B
【解析】试题分析：∵，
∴(a＋b)2＝ab，
即a2＋b2＋2ab＝ab，
a2＋b2＝－ab，
原式＝＝＝＝－1，
故选B． 计算：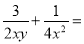 
________．
【解析】试题分析：原式＝
＝．
故答案为： ． 如图所示、△AOB和△COD均为等腰直角三角形，∠AOB=∠COD=90°，D在AB上．
（1）求证：△AOC≌△BOD；
（2）若AD=1，BD=2，求CD的长．
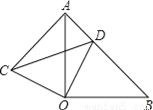
（1）证明见解析；（2）CD的长为．
【解析】（1）证明：如右图1，
，
又，
（2）由有： ， ，
，故 下列事件发生的可能性为0的是（ ）
A. 掷两枚骰子，同时出现数字“6”朝上
B. 小明从家里到学校用了10分钟，从学校回到家里却用了15分钟
C. 今天是星期天，昨天必定是星期六
D. 小明步行的速度是每小时40千米
D
【解析】对于A，掷两枚骰子，同时出现数字“6”朝上，可能性为；
对于B，小明从家里到学校用了10分钟，从学校回到家里却用了15分钟是可能是，比如去学校时下坡，则回家时上坡，当然回家比去学校用时多；
对于C，今天是星期天，昨天必定是星期六这是一个必然发生的事件，可能性为1；
对于D，小明步行的速度是每小时40千米，是不存在的.一般人步行的速度为3－5公里每小时，所以D发生...