题目内容
11.为培养学生良好学习习惯,某学校计划举行一次“整理错题集”的展示活动,对该校部分学生“整理错题集”的情况进行了一次抽样调查,根据收集的数据绘制了下面不完整的统计图表.| 整理情况 | 频数 | 频率 |
| 非常好 | 0.21 | |
| 较好 | 70 | 0.35 |
| 一般 | m | |
| 不好 | 36 |
(1)本次抽样共调查了200名学生;
(2)m=52;
(3)该校有1500名学生,估计该校学生整理错题集情况“非常好”和“较好”的学生一共约多少名?
(4)某学习小组4名学生的错题集中,有2本“非常好”(记为A1、A2),1本“较好”(记为B),1本“一般”(记为C),这些错题集封面无姓名,而且形状、大小、颜色等外表特征完全相同,从中抽取一本,不放回,从余下的3本错题集中再抽取一本,请用“列表法”或“画树形图”的方法求出两次抽到的错题集都是“非常好”的概率.
分析 (1)用较好的频数除以较好的频率.即可求出本次抽样调查的总人数;
(2)用总人数乘以非常好的频率,求出非常好的频数,再用总人数减去其它频数即可求出m的值;
(3)利用总人数乘以对应的频率即可;
(4)利用树形图方法,利用概率公式即可求解.
解答 解:(1)本次抽样共调查的人数是:70÷0.35=200(人);
(2)非常好的频数是:200×0.21=42(人),
一般的频数是:m=200-42-70-36=52(人),
(3)该校学生整理错题集情况“非常好”和“较好”的学生一共约有:1500×(0.21+0.35)=840(人);
(4)根据题意画图如下:
∵所有可能出现的结果共12种情况,并且每种情况出现的可能性相等,
其中两次抽到的错题集都是“非常好”的情况有2种,
∴两次抽到的错题集都是“非常好”的概率是$\frac{2}{12}$=$\frac{1}{6}$.
点评 此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
20.若二次函数y=2x2-2mx+2m-2的图象的顶点在x轴上,则m的值是( )
| A. | 2 | B. | -2 | C. | ±2 | D. | ±1 |
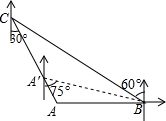 如图,“中海监50”正在南海海域A处巡逻,岛礁B上的中国海军发现点A在点B的正西方向上,岛瞧C上的中国海军发现点A在点C的南偏东30°方向上,已知点C在点B的北偏西60°方向上,且B、C两地相距150海里.
如图,“中海监50”正在南海海域A处巡逻,岛礁B上的中国海军发现点A在点B的正西方向上,岛瞧C上的中国海军发现点A在点C的南偏东30°方向上,已知点C在点B的北偏西60°方向上,且B、C两地相距150海里.
 2016年11月1日至6日,第十一届中国航展在广东珠海举行.在本次航展上,一架飞机飞行到A点时,测得观礼台C在飞机前下方,俯角为65°,此时飞机飞行路线改为沿坡脚30°的方向朝斜上方直线飞行,飞机飞行6km到达B处,此时飞机飞行高度为5km,另一个观礼台D恰好在飞机的正下方,求两个观礼台C与D之间的距离.
2016年11月1日至6日,第十一届中国航展在广东珠海举行.在本次航展上,一架飞机飞行到A点时,测得观礼台C在飞机前下方,俯角为65°,此时飞机飞行路线改为沿坡脚30°的方向朝斜上方直线飞行,飞机飞行6km到达B处,此时飞机飞行高度为5km,另一个观礼台D恰好在飞机的正下方,求两个观礼台C与D之间的距离.