题目内容
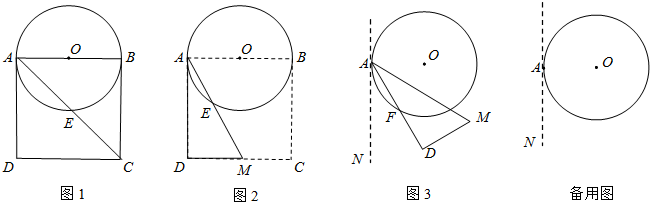
16.如图1,以边长为4的正方形纸片ABCD的边AB为直径作⊙O,交对角线AC于点E.(1)图1中,线段AE=2$\sqrt{2}$;
(2)如图2,在图1的基础上,以点A为端点作∠DAM=30°,交CD于点M,沿AM将四边形ABCM剪掉,使Rt△ADM绕点A逆时针旋转(如图3),设旋转角为α(0°<α<150°),在旋转过程中AD与⊙O交于点F.
①当α=30°时,请求出线段AF的长;
②当α=60°时,求出线段AF的长;判断此时DM与⊙O的位置关系,并说明理由;
③当α=90°时,DM与⊙O相切.
分析 (1)连接BE,由正方形的性质得出∠BAD=∠BAC=45°,由圆周角定理得出∠AEB=90°,证出△ABE是等腰直角三角形,由勾股定理得出AE=BE=$\frac{\sqrt{2}}{2}$AB=2$\sqrt{2}$;(2)①连接OA、OF,则OA=OF=2,证出∠OAF=90°-30°=60°,得出△OAF是等边三角形,即可得出AF=OA=2;
②证出∠NAM=90°,即AM⊥AN,得出AM过点O,设AM交⊙O于G,连接FG,过点O作OH⊥DM于H,由三角函数求出AF=AGcos∠DAM=2$\sqrt{3}$,在Rt△ADM中,求出AM=$\frac{8\sqrt{3}}{3}$,得出OM=AM-OA=$\frac{8\sqrt{3}}{3}$-2,在Rt△OHM中,由三角函数求出OH=4-$\sqrt{3}$,得出OH-OA=2-$\sqrt{3}$>0,得出OH>OA,即可证出DM与⊙O相离;
③当α=90°时,AD⊥AN,AD过圆心O,即可得出结论.
解答  解:(1)连接BE,如图1所示:
解:(1)连接BE,如图1所示:
∵四边形ABCD是正方形,
∴∠BAD=∠BAC=45°,
∵AB是⊙O的直径,
∴∠AEB=90°,
∴△ABE是等腰直角三角形,
∴AE=BE=$\frac{\sqrt{2}}{2}$AB=2$\sqrt{2}$;
故答案为:2$\sqrt{2}$;
(2)①连接OA、OF,如图3所示:
则OA=OF=2,
∵α=30°,
∴∠OAF=90°-30°=60°,
∴△OAF是等边三角形,
∴AF=OA=2;
②∵α=60°,∠DAN=30°,
∴∠NAM=90°,即AM⊥AN,
∴AM过点O,
设AM交⊙O于G,连接FG,过点O作OH⊥DM于H,如图4所示:
∴∠AFG=90°,∠OHM=90°,
∵AG=4,
∴AF=AGcos∠DAM=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$;
DM与⊙O相离,理由如下:
在Rt△ADM中,AM=$\frac{AD}{cos30°}$=$\frac{4}{\frac{\sqrt{3}}{2}}$=$\frac{8\sqrt{3}}{3}$,
∴OM=AM-OA=$\frac{8\sqrt{3}}{3}$-2,
在Rt△OHM中,OH=OM•sin∠OMH=($\frac{8\sqrt{3}}{3}$-2)×sin60°=4-$\sqrt{3}$,
∵OH-OA=4-$\sqrt{3}$-2=2-$\sqrt{3}$>0,
∴OH>OA,
∴DM与⊙O相离;
③当α=90°时,DM与⊙O相切.理由如下:
当α=90°时,AD⊥AN,AD过圆心O,
∵AD⊥DM,
∴DM与⊙O相切;
故答案为:90.
点评 本题是圆的综合题目,考查了正方形的性质、圆周角定理、等腰直角三角形的判定与性质、勾股定理、等边三角形的判定与性质、三角函数、直线与圆的位置关系、切线的判定等知识;本题综合性强,有一定难度.

 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案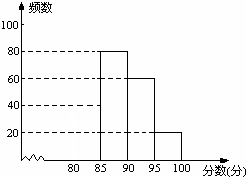 某校组织了一次环保知识竞赛活动,根据获奖同学在竞赛中的成绩制成的统计图表如下,仔细阅读图表解答问题:
某校组织了一次环保知识竞赛活动,根据获奖同学在竞赛中的成绩制成的统计图表如下,仔细阅读图表解答问题:| 分数段 | 频数 | 频率 |
| 80≤x<85 | a | 0.2 |
| 85≤x<90 | 80 | 0.4 |
| 90≤x<95 | 60 | b |
| 95≤x<100 | 20 | 0.1 |
(2)获奖成绩的中位数落在哪个分数段?
(3)估算全体获奖同学成绩的平均分.
| 整理情况 | 频数 | 频率 |
| 非常好 | 0.21 | |
| 较好 | 70 | 0.35 |
| 一般 | m | |
| 不好 | 36 |
(1)本次抽样共调查了200名学生;
(2)m=52;
(3)该校有1500名学生,估计该校学生整理错题集情况“非常好”和“较好”的学生一共约多少名?
(4)某学习小组4名学生的错题集中,有2本“非常好”(记为A1、A2),1本“较好”(记为B),1本“一般”(记为C),这些错题集封面无姓名,而且形状、大小、颜色等外表特征完全相同,从中抽取一本,不放回,从余下的3本错题集中再抽取一本,请用“列表法”或“画树形图”的方法求出两次抽到的错题集都是“非常好”的概率.
| A. | 5×102吨 | B. | 5×106吨 | C. | 5×107吨 | D. | 5×108吨 |
| A. | (a+b)2=a2+b2 | B. | (2a2)3=6a6 | C. | a3•a2=a6 | D. | $\sqrt{12}$-$\sqrt{3}$=$\sqrt{3}$ |
| A. | 四边都相等的四边形是矩形 | |
| B. | 菱形的对角线相等 | |
| C. | 对角线互相垂直的平行四边形是正方形 | |
| D. | 对角线相等的平行四边形是矩形 |

