题目内容
6.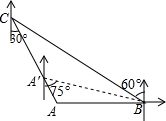 如图,“中海监50”正在南海海域A处巡逻,岛礁B上的中国海军发现点A在点B的正西方向上,岛瞧C上的中国海军发现点A在点C的南偏东30°方向上,已知点C在点B的北偏西60°方向上,且B、C两地相距150海里.
如图,“中海监50”正在南海海域A处巡逻,岛礁B上的中国海军发现点A在点B的正西方向上,岛瞧C上的中国海军发现点A在点C的南偏东30°方向上,已知点C在点B的北偏西60°方向上,且B、C两地相距150海里.(1)求出此时点A到岛礁C的距离;
(2)若“中海监50”从A处沿AC方向向岛礁C驶去,当到达点A′时,测得点B在A′的南偏东75°的方向上,求此时“中国海监50”的航行距离.(注:结果保留根号)
分析 (1)根据题意得出:∠CBD=30°,BC=150海里,再利用cos30°=$\frac{CD}{AC}$,进而求出答案;
(2)根据题意结合已知得出当点B在A′的南偏东75°的方向上,则A′B平分∠CBA,进而得出等式求出答案.
解答  解:(1)如图所示:延长BA,过点C作CD⊥BA延长线与点D,
解:(1)如图所示:延长BA,过点C作CD⊥BA延长线与点D,
由题意可得:∠CBD=30°,BC=150海里,
则DC=60海里,
故cos30°=$\frac{DC}{AC}$=$\frac{75}{AC}$=$\frac{\sqrt{3}}{2}$,
解得:AC=50$\sqrt{3}$,
答:点A到岛礁C的距离为50$\sqrt{3}$海里;
(2)如图所示:过点A′作A′N⊥BC于点N,
可得∠1=30°,∠BA′A=45°,
则∠2=15°,即A′B平分∠CBA,
设AA′=x,则A′E=$\frac{\sqrt{3}}{2}$x,
故CA′=2A′N=2×$\frac{\sqrt{3}}{2}$x=$\sqrt{3}$x,
∵$\sqrt{3}$x+x=50$\sqrt{3}$,
∴解得:x=75-25$\sqrt{3}$,
答:此时“中国海监50”的航行距离为(75-25$\sqrt{3}$)海里.
点评 此题主要考查了解直角三角形的应用,熟练应用锐角三角函数关系是解题关键.

练习册系列答案
相关题目
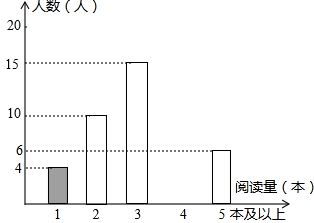
11.为培养学生良好学习习惯,某学校计划举行一次“整理错题集”的展示活动,对该校部分学生“整理错题集”的情况进行了一次抽样调查,根据收集的数据绘制了下面不完整的统计图表.
请根据图表中提供的信息,解答下列问题:
(1)本次抽样共调查了200名学生;
(2)m=52;
(3)该校有1500名学生,估计该校学生整理错题集情况“非常好”和“较好”的学生一共约多少名?
(4)某学习小组4名学生的错题集中,有2本“非常好”(记为A1、A2),1本“较好”(记为B),1本“一般”(记为C),这些错题集封面无姓名,而且形状、大小、颜色等外表特征完全相同,从中抽取一本,不放回,从余下的3本错题集中再抽取一本,请用“列表法”或“画树形图”的方法求出两次抽到的错题集都是“非常好”的概率.
| 整理情况 | 频数 | 频率 |
| 非常好 | 0.21 | |
| 较好 | 70 | 0.35 |
| 一般 | m | |
| 不好 | 36 |
(1)本次抽样共调查了200名学生;
(2)m=52;
(3)该校有1500名学生,估计该校学生整理错题集情况“非常好”和“较好”的学生一共约多少名?
(4)某学习小组4名学生的错题集中,有2本“非常好”(记为A1、A2),1本“较好”(记为B),1本“一般”(记为C),这些错题集封面无姓名,而且形状、大小、颜色等外表特征完全相同,从中抽取一本,不放回,从余下的3本错题集中再抽取一本,请用“列表法”或“画树形图”的方法求出两次抽到的错题集都是“非常好”的概率.
15.已知一次函数y=-$\frac{1}{2}$x+2,当1≤x≤4时,y的最大值是( )
| A. | 2 | B. | $\frac{3}{2}$ | C. | $\frac{5}{2}$ | D. | -6 |
16.将抛物线y=x2+4x+3沿y轴向右平移3个单位,然后再向上平移5个单位后所得抛物线的顶点坐标是( )
| A. | (5,7) | B. | (-1,7) | C. | (1,4) | D. | (5,4) |
 用6个完全相同的小正方体组合成如图所示的立体图形,它的左视图为( )
用6个完全相同的小正方体组合成如图所示的立体图形,它的左视图为( )



