题目内容
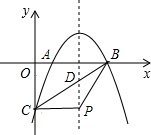 如图:抛物线y=ax2-4ax+m与x轴交于A、B两点,点A的坐标是(1,0),与y轴交于点C.
如图:抛物线y=ax2-4ax+m与x轴交于A、B两点,点A的坐标是(1,0),与y轴交于点C.(1)求抛物线的对称轴和点B的坐标;
(2)过点C作CP⊥对称轴于点P,连接BC交对称轴于点D,连接AC、BP,且∠BPD=∠BCP,求抛物线的解析式.
考点:二次函数综合题
专题:
分析:(1)由抛物线y=ax2-4ax+m的对称轴公式x=-
,即可求得其对称轴,又由点A、B关于对称轴对称,即可求得点B的坐标;
(2)由点A(1,0),B(3,0),求得AB的值,又由CP⊥对称轴,可得CP∥AB,易证得四边形ABPC是平行四边形,然后设点C(0,x)(x<0),证得△BPD∽△BCP,根据相似三角形的对应边成比例,即可求得x的值,又由二次函数过点A与C,利用待定系数法即可求得此抛物线的解析式.
| b |
| 2a |
(2)由点A(1,0),B(3,0),求得AB的值,又由CP⊥对称轴,可得CP∥AB,易证得四边形ABPC是平行四边形,然后设点C(0,x)(x<0),证得△BPD∽△BCP,根据相似三角形的对应边成比例,即可求得x的值,又由二次函数过点A与C,利用待定系数法即可求得此抛物线的解析式.
解答:解:(1)对称轴是x=-
=2,
∵点A(1,0)且点A、B关于x=2对称,
∴点B(3,0);
(2)点A(1,0),B(3,0),
∴AB=2,
∵CP⊥对称轴于P,
∴CP∥AB,
∵对称轴是x=2,
∴AB∥CP且AB=CP,
∴四边形ABPC是平行四边形,
设点C(0,x)(x<0),
在Rt△AOC中,AC=
,
∴BP=
,
在Rt△BOC中,BC=
,
∵
=
=
,
∴BD=
,
∵∠BPD=∠BCP 且∠PBD=∠CBP,
∴△BPD∽△BCP,
∴BP2=BD•BC,
即(
)2=
•
,
∴x2+1=
(x2+9),
∴x1=
,x2=-
,
∵点C在y轴的负半轴上,
∴点C(0,-
),
∴y=ax2-4ax-
,
∵过点(1,0),
∴a-4a-
=0,
解得:a=-
.
∴抛物线解析式是:y=-
x2+
x-
.
| b |
| 2a |
∵点A(1,0)且点A、B关于x=2对称,
∴点B(3,0);
(2)点A(1,0),B(3,0),
∴AB=2,
∵CP⊥对称轴于P,
∴CP∥AB,
∵对称轴是x=2,
∴AB∥CP且AB=CP,
∴四边形ABPC是平行四边形,
设点C(0,x)(x<0),
在Rt△AOC中,AC=
| x2+1 |

∴BP=
| x2+1 |
在Rt△BOC中,BC=
| x2+9 |
∵
| BD |
| BC |
| BE |
| BO |
| 1 |
| 3 |
∴BD=
| 1 |
| 3 |
| x2+9 |
∵∠BPD=∠BCP 且∠PBD=∠CBP,
∴△BPD∽△BCP,
∴BP2=BD•BC,
即(
| x2+1 |
| 1 |
| 3 |
| x2+9 |
| x2+9 |
∴x2+1=
| 1 |
| 3 |
∴x1=
| 3 |
| 3 |
∵点C在y轴的负半轴上,
∴点C(0,-
| 3 |
∴y=ax2-4ax-
| 3 |
∵过点(1,0),
∴a-4a-
| 3 |
解得:a=-
| ||
| 3 |
∴抛物线解析式是:y=-
| ||
| 3 |
4
| ||
| 3 |
| 3 |
点评:此题考查了二次函数对称轴的求解方法,二次函数的对称性,待定系数法求函数的解析式以及相似三角形的判定与性质等知识.此题综合性很强,难度较大,解题的关键是注意数形结合的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
与-
互为相反数的是( )
| 1 |
| 2 |
| A、-0.5 | ||
B、
| ||
| C、2 | ||
D、
|

 如图,⊙O1和⊙O2外切于点P,O1 O2的延长线交⊙O2于点A,AB切⊙O1于点B,交⊙O2于点C.BE是⊙O1的直径,连结PE,过点B作BF⊥O1P,垂足为F,延长BF交PE于点G,连结BP.
如图,⊙O1和⊙O2外切于点P,O1 O2的延长线交⊙O2于点A,AB切⊙O1于点B,交⊙O2于点C.BE是⊙O1的直径,连结PE,过点B作BF⊥O1P,垂足为F,延长BF交PE于点G,连结BP.