题目内容
探究发现:阅读解答题:在数学中,有些大数值问题可以通过用字母代替数转化成整式问题来解决.例:试比较20142015×20142012与20142014×20142013的大小.
解:设20142014=a,x=20142015×20142012,
y=20142014×20142013
那么x=(a+1)(a-2),
那么y=a(a-1)
∵x-y=
∴x y(填>、<).
填完后,你学到了这种方法吗?不妨尝试一下,相信你准行!
问题:计算(m+22.2014)(m+14.2014)-(m+18.2014)(m+17.2014).

解:设20142014=a,x=20142015×20142012,
y=20142014×20142013
那么x=(a+1)(a-2),
那么y=a(a-1)
∵x-y=
∴x
填完后,你学到了这种方法吗?不妨尝试一下,相信你准行!
问题:计算(m+22.2014)(m+14.2014)-(m+18.2014)(m+17.2014).
考点:整式的混合运算
专题:阅读型
分析:根据题意列出关系式,去括号合并即可得到结果;计算(m+22.2014)(m+14.2014)-(m+18.2014)(m+17.2014)的结果,可令m+18.2014=x,再结合平方差公式计算得到结果.
解答:解:x-y=(a+1)(a-2)-a(a-1)=a2-a-2-a2+a=-2;
∴x-y=-2<0,即x<y;
设m+18.2014=x,则有:
原式=(x+4)(x-4)-x(x-1)
=x2-16-x2+x
=x-16
=m+18.2014-16
=m+2.2014
故答案为:-2,<;m+2.2014.
∴x-y=-2<0,即x<y;
设m+18.2014=x,则有:
原式=(x+4)(x-4)-x(x-1)
=x2-16-x2+x
=x-16
=m+18.2014-16
=m+2.2014
故答案为:-2,<;m+2.2014.
点评:本题考查了单项式乘多项式,平方差公式,读懂题目信息,找出其运算方法是解题的关键.

练习册系列答案
相关题目
已知a=234,b=243,c=324,d=432,e=423,则a,b,c,d,e的大小关系是( )
| A、a=b=d=e<c |
| B、a=b=d=e>c |
| C、e<d<c<b<a |
| D、e<c<d<b<a |
-2的相反数是( )
A、
| ||
B、-
| ||
| C、2 | ||
| D、-2 |
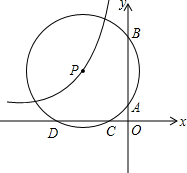 如图,⊙P与两坐标轴分别交于点A(0,2)、B(0,6)、C(-3,0)和D,双曲线y=
如图,⊙P与两坐标轴分别交于点A(0,2)、B(0,6)、C(-3,0)和D,双曲线y=| k |
| x |
| A、-14 | B、-12 |
| C、14 | D、12 |
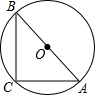 如图,AB是⊙O的直径,∠B=45°,AB=2,则∠C=
如图,AB是⊙O的直径,∠B=45°,AB=2,则∠C=
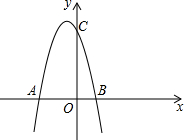 如图、已知抛物线与x轴交于点A(-4,0),B(2,0),与y轴交点C(0,8).
如图、已知抛物线与x轴交于点A(-4,0),B(2,0),与y轴交点C(0,8).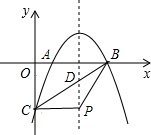 如图:抛物线y=ax2-4ax+m与x轴交于A、B两点,点A的坐标是(1,0),与y轴交于点C.
如图:抛物线y=ax2-4ax+m与x轴交于A、B两点,点A的坐标是(1,0),与y轴交于点C.