题目内容
如果我们定义:“到三角形的两个顶点距离相等的点,叫做此三角形的开心点.”那么:
(1)如图1,观察并思考,△ABC的开心点有 个;
(2)如图2,CD为等边三角形ABC的高,开心点P在高CD上,且PD=
AB,则∠APB的度数为 ;
(3)已知△ABC为直角三角形,斜边BC=5,AB=3,开心点P在AC边上,试探究PA的长.
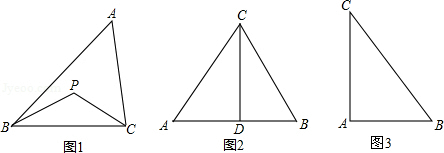
(1)如图1,观察并思考,△ABC的开心点有
(2)如图2,CD为等边三角形ABC的高,开心点P在高CD上,且PD=
| 1 |
| 2 |
(3)已知△ABC为直角三角形,斜边BC=5,AB=3,开心点P在AC边上,试探究PA的长.

考点:角平分线的性质,等边三角形的性质,勾股定理
专题:
分析:(1)根据到线段两端点距离相等的点在线段的垂直平分线判断开心点有无数个;
(2)根据等边三角形的性质可得BD=
AB,然后判断出△PBD是等腰直角三角形,再根据等边三角形的对称性可得∠APB=2∠BPD;
(3)利用勾股定理列式求出AC,再分①PB=PC,②PA=PC,③PA=PB三种情况讨论求解.
(2)根据等边三角形的性质可得BD=
| 1 |
| 2 |
(3)利用勾股定理列式求出AC,再分①PB=PC,②PA=PC,③PA=PB三种情况讨论求解.
解答:解:(1)边AB、BC、AC三边的垂直平分线上的点都是开心点,
所以,有无数个开心点;
(2)∵CD为等边△ABC的高,
∴BD=
AB,
∵开心点P在高CD上,且PD=
AB,
∴△PBD是等腰直角三角形,
∴∠BPD=45°,
由等边三角形的对称性,∠APB=2∠BPD=2×45°=90°;
故答案为:(1)无数;(2)90°;
(3)解:在Rt△ABC中,BC=5,AB=3,
∴AC=
=
=4,
①若PB=PC,设PA=x,则x2+32=(4-x)2,
∴x=
,
即PA=
,
②若PA=PC,则PA=2,
③若PA=PB,在Rt△PAB中,不可能,
综上所述,PA=2或
.
所以,有无数个开心点;
(2)∵CD为等边△ABC的高,
∴BD=
| 1 |
| 2 |
∵开心点P在高CD上,且PD=
| 1 |
| 2 |
∴△PBD是等腰直角三角形,
∴∠BPD=45°,
由等边三角形的对称性,∠APB=2∠BPD=2×45°=90°;
故答案为:(1)无数;(2)90°;
(3)解:在Rt△ABC中,BC=5,AB=3,
∴AC=
| BC2-AB2 |
| 52-32 |
①若PB=PC,设PA=x,则x2+32=(4-x)2,
∴x=
| 7 |
| 8 |
即PA=
| 7 |
| 8 |
②若PA=PC,则PA=2,
③若PA=PB,在Rt△PAB中,不可能,
综上所述,PA=2或
| 7 |
| 8 |
点评:本题考查了线段垂直平分线上的点到两端点的距离相等的性质,等边三角形的性质,勾股定理,读懂题目信息,理解“开心点”的定义是解题的关键,难点在于(3)分情况讨论.

练习册系列答案
相关题目
在一个不透明的口袋中装有若干个除颜色不同其余都相同的球,如果口袋中装有5个白球,且摸到白球的概率为
,那么口袋中球的总数为( )
| 1 |
| 3 |
| A、15个 | B、12个 |
| C、9个 | D、6个 |
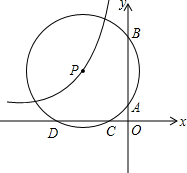 如图,⊙P与两坐标轴分别交于点A(0,2)、B(0,6)、C(-3,0)和D,双曲线y=
如图,⊙P与两坐标轴分别交于点A(0,2)、B(0,6)、C(-3,0)和D,双曲线y=| k |
| x |
| A、-14 | B、-12 |
| C、14 | D、12 |
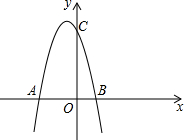 如图、已知抛物线与x轴交于点A(-4,0),B(2,0),与y轴交点C(0,8).
如图、已知抛物线与x轴交于点A(-4,0),B(2,0),与y轴交点C(0,8). 如图,点A、B、C是⊙O上的三点,AB∥OC.
如图,点A、B、C是⊙O上的三点,AB∥OC.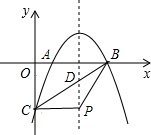 如图:抛物线y=ax2-4ax+m与x轴交于A、B两点,点A的坐标是(1,0),与y轴交于点C.
如图:抛物线y=ax2-4ax+m与x轴交于A、B两点,点A的坐标是(1,0),与y轴交于点C. 如图,抛物线y=ax2+bx+8(a≠0)与x轴交于点A(-2,0)、点B,与y轴交于点C,顶点为D,tan∠ABC=2.
如图,抛物线y=ax2+bx+8(a≠0)与x轴交于点A(-2,0)、点B,与y轴交于点C,顶点为D,tan∠ABC=2. 如图,已知△ABC中,∠1=∠2,AE=AD,求证:DF=EF.
如图,已知△ABC中,∠1=∠2,AE=AD,求证:DF=EF.