题目内容
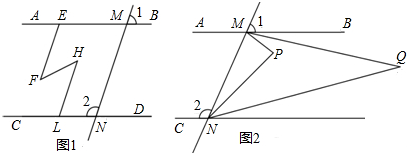
已知:如图1,∠1+∠2=180°,∠AEF=∠HLN;
(1)判断图中平行的直线,并给予证明;
(2)如图2,∠PMQ=2∠QMB,∠PNQ=2∠QND,请判断∠P与∠Q的数量关系,并证明.
(1)判断图中平行的直线,并给予证明;
(2)如图2,∠PMQ=2∠QMB,∠PNQ=2∠QND,请判断∠P与∠Q的数量关系,并证明.

考点:平行线的判定与性质
专题:
分析:(1)求出∠AMN+∠2=180°,根据平行线的判定推出AB∥CD即可;根据平行线性质和已知求出∠AEF=∠EF1L,根据平行线的判定推出即可;
(2)根据平行线的性质得出∠RQM=∠QMB,RQ∥CD,推出∠MQN=∠QMB+∠QND,同理∠MRN=∠PMB+∠PND,代入求出即可.
(2)根据平行线的性质得出∠RQM=∠QMB,RQ∥CD,推出∠MQN=∠QMB+∠QND,同理∠MRN=∠PMB+∠PND,代入求出即可.
解答:解:(1)AB∥CD,EF∥HL,
证明如下:∵∠1=∠AMN,
∴∠1+∠2=180°,
∴∠AMN+∠2=180°,
∴AB∥CD;
延长EF交CD于F1,
∵AB∥CD,∠AEF=∠HLN,
∴∠AEF=∠EF1L,
∴EF∥HL;

(2)∠P=3∠Q,
证明如下:∵AB∥CD,作QR∥AB,PL∥AB,
∴∠RQM=∠QMB,RQ∥CD,
∴∠RQN=∠QND,
∴∠MQN=∠QMB+∠QND,
∵AB∥CD,PL∥AB,
∴AB∥CD∥PL,
∴∠MPL=∠PMB,∠NPL=∠PND,
∴∠MRN=∠PMB+∠PND,
∵∠PMQ=2∠QMB,∠PNQ=2∠QND,
∴∠PMB=3∠QMB,∠PND=3∠QND,
∴∠MRN=3∠MQN,
即∠P=3∠Q;
证明如下:∵∠1=∠AMN,
∴∠1+∠2=180°,
∴∠AMN+∠2=180°,
∴AB∥CD;
延长EF交CD于F1,
∵AB∥CD,∠AEF=∠HLN,
∴∠AEF=∠EF1L,
∴EF∥HL;

(2)∠P=3∠Q,
证明如下:∵AB∥CD,作QR∥AB,PL∥AB,
∴∠RQM=∠QMB,RQ∥CD,
∴∠RQN=∠QND,
∴∠MQN=∠QMB+∠QND,
∵AB∥CD,PL∥AB,
∴AB∥CD∥PL,
∴∠MPL=∠PMB,∠NPL=∠PND,
∴∠MRN=∠PMB+∠PND,
∵∠PMQ=2∠QMB,∠PNQ=2∠QND,
∴∠PMB=3∠QMB,∠PND=3∠QND,
∴∠MRN=3∠MQN,
即∠P=3∠Q;
点评:本题考查了平行线的性质和判定的应用,主要考查学生运用性质进行推理的能力.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
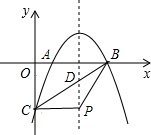 如图:抛物线y=ax2-4ax+m与x轴交于A、B两点,点A的坐标是(1,0),与y轴交于点C.
如图:抛物线y=ax2-4ax+m与x轴交于A、B两点,点A的坐标是(1,0),与y轴交于点C.
 如图,已知△ABC中,∠1=∠2,AE=AD,求证:DF=EF.
如图,已知△ABC中,∠1=∠2,AE=AD,求证:DF=EF.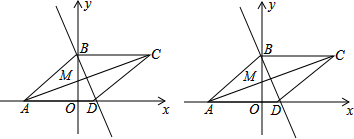
 已知:D在格点上,每个小正方形的边长为1,
已知:D在格点上,每个小正方形的边长为1,