题目内容
 如图,在△ABC中,AB=AC,AD是∠BAC的平分线,将△ABC绕点C按顺时针方向旋转,点B落到AD上的点B1处得△A1B1C,点E是AB1的中点,连接A1E,求证:
如图,在△ABC中,AB=AC,AD是∠BAC的平分线,将△ABC绕点C按顺时针方向旋转,点B落到AD上的点B1处得△A1B1C,点E是AB1的中点,连接A1E,求证:(1)∠B1CB=60°;
(2)A1E∥BC.
考点:旋转的性质,全等三角形的判定与性质,等边三角形的判定与性质
专题:证明题
分析:(1)连接BB1,如图,先根据等腰三角形的性质证明AD垂直平分BC,得到B1B=B1C,再利用旋转的性质得到CB1=CB,于是可证明△B1BC为等边三角形,
然后根据等边三角形的性质可得∠B1CB=60°;
(2)先根据旋转的性质得∠A1CA=∠B1CB=60°,CA1=CA,AB=A1B1,则可判断△AA1C为等边三角形,得到CA=AA1,加上AB=AC,所以AA1=A1B1,由于点E是AB1的中点,根据等腰三角形的性质得到A1E⊥AB1,然后利用平行线的性质可得到结论.
然后根据等边三角形的性质可得∠B1CB=60°;
(2)先根据旋转的性质得∠A1CA=∠B1CB=60°,CA1=CA,AB=A1B1,则可判断△AA1C为等边三角形,得到CA=AA1,加上AB=AC,所以AA1=A1B1,由于点E是AB1的中点,根据等腰三角形的性质得到A1E⊥AB1,然后利用平行线的性质可得到结论.
解答: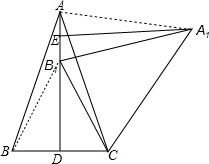 证明:(1)连接BB1,如图,
证明:(1)连接BB1,如图,
∵AB=AC,AD是∠BAC的平分线,
∴AD⊥BC,BD=CD,
∴AD垂直平分BC,
∴B1B=B1C,
∴△ABC绕点C按顺时针方向旋转,点B落到AD上的点B1处得△A1B1C,
∴CB1=CB,
∴B1B=B1C=BC,
∴△B1BC为等边三角形,
∴∠B1CB=60°;
(2)∵△ABC绕点C按顺时针方向旋转,点B落到AD上的点B1处得△A1B1C,
∴∠A1CA=∠B1CB=60°,CA1=CA,AB=A1B1,
∴△AA1C为等边三角形,
∴CA=AA1,
而AB=AC,
∴AA1=A1B1,
而点E是AB1的中点,
∴A1E⊥AB1,
∵BC⊥AD,
∴A1E∥BC.
 证明:(1)连接BB1,如图,
证明:(1)连接BB1,如图,∵AB=AC,AD是∠BAC的平分线,
∴AD⊥BC,BD=CD,
∴AD垂直平分BC,
∴B1B=B1C,
∴△ABC绕点C按顺时针方向旋转,点B落到AD上的点B1处得△A1B1C,
∴CB1=CB,
∴B1B=B1C=BC,
∴△B1BC为等边三角形,
∴∠B1CB=60°;
(2)∵△ABC绕点C按顺时针方向旋转,点B落到AD上的点B1处得△A1B1C,
∴∠A1CA=∠B1CB=60°,CA1=CA,AB=A1B1,
∴△AA1C为等边三角形,
∴CA=AA1,
而AB=AC,
∴AA1=A1B1,
而点E是AB1的中点,
∴A1E⊥AB1,
∵BC⊥AD,
∴A1E∥BC.
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等腰三角形的性质和等边三角形的判定与性质.

练习册系列答案
相关题目
 如图,△ABD≌△CBD,若∠A=80°,∠ABC=70°,则∠BDC的度数为
如图,△ABD≌△CBD,若∠A=80°,∠ABC=70°,则∠BDC的度数为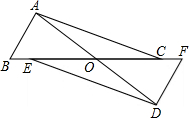 已知,如图,AD、BF相交于O点,点E、C在BF上,且BE=FC,AC=DE,AB=DF.求证:
已知,如图,AD、BF相交于O点,点E、C在BF上,且BE=FC,AC=DE,AB=DF.求证: 已知:⊙O和⊙O′交于A、B两点,过点B的直线分别交⊙O和⊙O′于点C、D、G是两圆外一点,GC、GD分别交⊙O和⊙O′于点E、F,求证:∠EAF=∠C+∠D.
已知:⊙O和⊙O′交于A、B两点,过点B的直线分别交⊙O和⊙O′于点C、D、G是两圆外一点,GC、GD分别交⊙O和⊙O′于点E、F,求证:∠EAF=∠C+∠D.
 如图,AB=CD,AD=BC,O为BD上任意一点,过O点的直线分别交AD、BC于M、N两点.求证:∠1=∠2.
如图,AB=CD,AD=BC,O为BD上任意一点,过O点的直线分别交AD、BC于M、N两点.求证:∠1=∠2. 如图,两个同心圆的半径分别为2cm和4cm,有大圆上一点A作小圆的两条切线AB、AC,切点为B、C,求图中阴影部分的面积.
如图,两个同心圆的半径分别为2cm和4cm,有大圆上一点A作小圆的两条切线AB、AC,切点为B、C,求图中阴影部分的面积.