题目内容
已知A(2,2),B(7,4),若要在x轴上找到一点P,使AP+BP最短,由此得点P的坐标为 ,AP+BP和的最短值为 .
考点:轴对称-最短路线问题,坐标与图形性质
专题:
分析:先根据关于x轴对称的点的坐标特点得出点A关于x轴对称点A′的坐标,连接A′B,则A′B的长即为AP+BP和的最短值,利用两点间的距离公式求出A′B的长,再用待定系数法求出直线A′B的解析式即可得出P点坐标.
解答: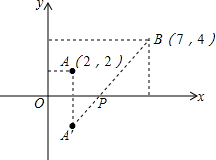 解:如图所示,
解:如图所示,
作点A关于x轴的对称点A′,连接A′B交x轴于点P,则P点即为所求点.
∵A(2,2),
∴A′(2,-2),
∴A′B=
=
.
设直线A′B的解析式为y=kx+b(k≠0),
∴
,
解得
,
∴直线A′B的解析式为y=
x-
,
∴P(
,0).
故答案为:(
,0),
.
 解:如图所示,
解:如图所示,作点A关于x轴的对称点A′,连接A′B交x轴于点P,则P点即为所求点.
∵A(2,2),
∴A′(2,-2),
∴A′B=
| (2-7)2+(-2-4)2 |
| 61 |
设直线A′B的解析式为y=kx+b(k≠0),
∴
|
解得
|
∴直线A′B的解析式为y=
| 6 |
| 5 |
| 22 |
| 5 |
∴P(
| 11 |
| 3 |
故答案为:(
| 11 |
| 3 |
| 61 |
点评:本题考查的是轴对称-最短路线问题,熟知“两点之间,线段最短”是解答此题的关键.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
某厂一月份生产某机器300台,计划二、三月份共生产980台.设二三月份每月的平均增长率为x,根据题意列出的方程是( )
| A、300(1+x)2=980 |
| B、300(1+x)+300(1+x)2=980 |
| C、300(1-x)2=980 |
| D、300+300(1+x)+300(1+x)2=980 |
 如图,在△ABC中,AB=AC,AD是∠BAC的平分线,将△ABC绕点C按顺时针方向旋转,点B落到AD上的点B1处得△A1B1C,点E是AB1的中点,连接A1E,求证:
如图,在△ABC中,AB=AC,AD是∠BAC的平分线,将△ABC绕点C按顺时针方向旋转,点B落到AD上的点B1处得△A1B1C,点E是AB1的中点,连接A1E,求证:
 如图为正方形空地的绿化带设计方案,阴影部分为绿化带,根据题中给出的数据,分别就两种方案表示出绿化带的面积.
如图为正方形空地的绿化带设计方案,阴影部分为绿化带,根据题中给出的数据,分别就两种方案表示出绿化带的面积.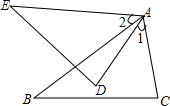 已知:如图,AB=AE,∠1=∠2,AD=AC
已知:如图,AB=AE,∠1=∠2,AD=AC