题目内容
如图，AB=CD，AD=BC，O为BD上任意一点，过O点的直线分别交AD、BC于M、N两点．求证：∠1=∠2．考点：全等三角形的判定与性质
专题：证明题
分析：根据题干中给出的AB=CD，AD=BC可以求证△ABD≌△CDB，可以求得∠ADB=∠CBD，可以求得∠1=∠2．
解答：解：在△ABD和△CDB中，
，
∴△ABD≌△CDB（SSS），
∴∠ADB=∠CBD，
∵∠MOD=∠NOB，∠1=180°-∠MOD-∠ADB；∠2=180°-∠NOB-∠CBD；
∴∠1=∠2．
|
∴△ABD≌△CDB（SSS），
∴∠ADB=∠CBD，
∵∠MOD=∠NOB，∠1=180°-∠MOD-∠ADB；∠2=180°-∠NOB-∠CBD；
∴∠1=∠2．
点评：本题考查了全等三角形的判定，考查了全等三角形对应角相等的性质，本题中求证全等三角形是解题的关键．
练习册系列答案
相关题目
方程x2-2=0的解为（ ）
| A、2 | ||||
B、
| ||||
| C、2与-2 | ||||
D、
|
如图，在△ABC中，AB=AC，AD是∠BAC的平分线，将△ABC绕点C按顺时针方向旋转，点B落到AD上的点B1处得△A1B1C，点E是AB1的中点，连接A1E，求证：
如图为正方形空地的绿化带设计方案，阴影部分为绿化带，根据题中给出的数据，分别就两种方案表示出绿化带的面积．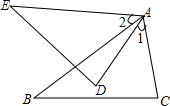
已知：如图，AB=AE，∠1=∠2，AD=AC
