题目内容
已知：⊙O和⊙O′交于A、B两点，过点B的直线分别交⊙O和⊙O′于点C、D、G是两圆外一点，GC、GD分别交⊙O和⊙O′于点E、F，求证：∠EAF=∠C+∠D．考点：相交两圆的性质
专题：证明题
分析：连接BA并延长，由圆内接四边形的性质可知∠D=∠GAF，∠C=∠GAE，由此可得出结论．
解答：
解：连接BA并延长，
∵四边形ABDF内接与⊙O′，
∴∠D=∠GAF，
同理，∠C=∠GAE，
∴∠EAF=∠GAF+∠GAE=∠C+∠D．
解：连接BA并延长，∵四边形ABDF内接与⊙O′，
∴∠D=∠GAF，
同理，∠C=∠GAE，
∴∠EAF=∠GAF+∠GAE=∠C+∠D．
点评：本题考查的是相交两圆的性质，根据题意作出辅助线，构造出圆内接四边形是解答此题的关键．
练习册系列答案
相关题目
如图，在△ABC中，D为BC的中点，DE⊥DF交AB、AC于E、F，求证：BE+CF＞EF．
如图，在△ABC中，AB=AC，AD是∠BAC的平分线，将△ABC绕点C按顺时针方向旋转，点B落到AD上的点B1处得△A1B1C，点E是AB1的中点，连接A1E，求证：
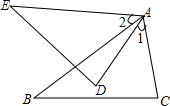已知：如图，AB=AE，∠1=∠2，AD=AC