题目内容
 如图,两个同心圆的半径分别为2cm和4cm,有大圆上一点A作小圆的两条切线AB、AC,切点为B、C,求图中阴影部分的面积.
如图,两个同心圆的半径分别为2cm和4cm,有大圆上一点A作小圆的两条切线AB、AC,切点为B、C,求图中阴影部分的面积.考点:切线的性质
专题:
分析:作辅助线,构造直角三角形,根据边角关系求出圆心角∠BOC,进而求出由优弧
所围成的扇形面积;求出四边形ABOC的面积问题即可解决.
 |
| BmC |
解答: 解:如图,连接OA、OB、OC;
解:如图,连接OA、OB、OC;
∵AB、AC分别是小⊙O的切线,
∴OB⊥AB,OC⊥AC;
又∵OB=2cm,OA=4cm,
∴OB=
OA,
∴∠BAO=30°,∠AOB=90°-30°=60°;
同理可证∠AOC=60°;
∴优弧
的度数=360°-120°=240°;
设由优弧
,半径OB、OC所围成的扇形的面积为S;
则S=
=
(cm2);
在△AOB与△AOC中,
∵
,
∴△AOB≌△AOC(AAS),
∴S四边形ABOC=2S△AOB;
由勾股定理得:AB=
=
=2
,
∴S△AOB=
AB•OB=
×2
×2=2
,
∴图中阴影部分的面积
=
+2×2
=
+4
(cm2).
 解:如图,连接OA、OB、OC;
解:如图,连接OA、OB、OC; ∵AB、AC分别是小⊙O的切线,
∴OB⊥AB,OC⊥AC;
又∵OB=2cm,OA=4cm,
∴OB=
| 1 |
| 2 |
∴∠BAO=30°,∠AOB=90°-30°=60°;
同理可证∠AOC=60°;
∴优弧
 |
| BmC |
设由优弧
 |
| BmC |
则S=
| 120π×2 |
| 360 |
| 2π |
| 3 |
在△AOB与△AOC中,
∵
|
∴△AOB≌△AOC(AAS),
∴S四边形ABOC=2S△AOB;
由勾股定理得:AB=
| 42-22 |
| 12 |
| 3 |
∴S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∴图中阴影部分的面积
=
| 2π |
| 3 |
| 3 |
=
| 2π |
| 3 |
| 3 |
点评:该题主要考查了圆的切线的性质定理及其应用问题;解题的关键是作出辅助线,灵活运用扇形的面积公式及三角形的面积公式来解题.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
 如图,在△ABC中,AB=AC,AD是∠BAC的平分线,将△ABC绕点C按顺时针方向旋转,点B落到AD上的点B1处得△A1B1C,点E是AB1的中点,连接A1E,求证:
如图,在△ABC中,AB=AC,AD是∠BAC的平分线,将△ABC绕点C按顺时针方向旋转,点B落到AD上的点B1处得△A1B1C,点E是AB1的中点,连接A1E,求证:
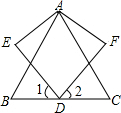 如图,△ABC中,AB=AC,D是BC的中点,∠AED=∠AFD=90°,AE=AF.
如图,△ABC中,AB=AC,D是BC的中点,∠AED=∠AFD=90°,AE=AF.