题目内容
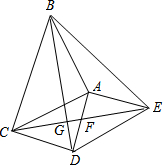 如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连接CE交AD于点F,连接BD交CE于点G,连接BE;下列结论中:①CE=BD;②∠ADB=∠AEB;③△ADC是等腰直角三角形;④CD•AE=EF•CG;一定正确的结论有( )
如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连接CE交AD于点F,连接BD交CE于点G,连接BE;下列结论中:①CE=BD;②∠ADB=∠AEB;③△ADC是等腰直角三角形;④CD•AE=EF•CG;一定正确的结论有( )| A、1个 | B、2个 | C、3个 | D、4个 |
考点:全等三角形的判定与性质,等腰直角三角形,相似三角形的判定与性质
专题:
分析:①利用SAS证明△BAD≌△CAE,可得到CE=BD;
③利用SAS证明△BAE≌△BAD可得到∠ADB=∠AEB;
③利用平行四边形的性质可得AE=CD,再结合△ADE是等腰直角三角形可得到△ADC是等腰直角三角形;
④利用已知得出∠GFD=∠AFE,以及∠GDF+∠GFD=90°,得出∠GCD=∠AEF,进而得出△CGD∽△EAF,得出比例式;即可得出结论.
③利用SAS证明△BAE≌△BAD可得到∠ADB=∠AEB;
③利用平行四边形的性质可得AE=CD,再结合△ADE是等腰直角三角形可得到△ADC是等腰直角三角形;
④利用已知得出∠GFD=∠AFE,以及∠GDF+∠GFD=90°,得出∠GCD=∠AEF,进而得出△CGD∽△EAF,得出比例式;即可得出结论.
解答: 解:①∵∠BAC=∠DAE=90°,
解:①∵∠BAC=∠DAE=90°,
∴∠BAC+∠DAC=∠DAE+∠DAC,
即:∠BAD=∠CAE,
∵△ABC和△ADE都是等腰直角三角形,
∴AB=AC,AE=AD,
∴△BAD≌△CAE(SAS),
∴CE=BD,
∴故①正确;
②∵△ADC是等腰直角三角形,
∴∠CAD=45°,
∴∠BAD=90°+45°=135°,
∵∠EAD=∠BAC=90°,∠CAD=45°,
∴∠BAE=360°-90°-90°-45°=135°,
又AB=AB,AD=AE,
∴△BAE≌△BAD(SAS),
∴∠ADB=∠AEB;
故②正确;
③∵四边形ACDE是平行四边形,
∴∠EAD=∠ADC=90°,AE=CD,
∵△ADE是等腰直角三角形,
∴AE=AD,
∴AD=CD,
∴△ADC是等腰直角三角形,
∴③正确;
④∵△BAD≌△CAE,△BAE≌△BAD,
∴△CAE≌△BAE,
∴∠BEA=∠CEA=∠BDA,
∵∠AEF+∠AFE=90°,
∴∠AFE+∠BEA=90°,
∵∠GFD=∠AFE,∠ADB=∠AEB,
∴∠ADB+∠GFD=90°,
∴∠CGD=90°,
∵∠FAE=90°,∠GCD=∠AEF,
∴△CGD∽△EAF,
∴
=
,
∴CD•AE=EF•CG.
故④正确,
故正确的有4个.
故选:D.
 解:①∵∠BAC=∠DAE=90°,
解:①∵∠BAC=∠DAE=90°,∴∠BAC+∠DAC=∠DAE+∠DAC,
即:∠BAD=∠CAE,
∵△ABC和△ADE都是等腰直角三角形,
∴AB=AC,AE=AD,
∴△BAD≌△CAE(SAS),
∴CE=BD,
∴故①正确;
②∵△ADC是等腰直角三角形,
∴∠CAD=45°,
∴∠BAD=90°+45°=135°,
∵∠EAD=∠BAC=90°,∠CAD=45°,
∴∠BAE=360°-90°-90°-45°=135°,
又AB=AB,AD=AE,
∴△BAE≌△BAD(SAS),
∴∠ADB=∠AEB;
故②正确;
③∵四边形ACDE是平行四边形,
∴∠EAD=∠ADC=90°,AE=CD,
∵△ADE是等腰直角三角形,
∴AE=AD,
∴AD=CD,
∴△ADC是等腰直角三角形,
∴③正确;
④∵△BAD≌△CAE,△BAE≌△BAD,
∴△CAE≌△BAE,
∴∠BEA=∠CEA=∠BDA,
∵∠AEF+∠AFE=90°,
∴∠AFE+∠BEA=90°,
∵∠GFD=∠AFE,∠ADB=∠AEB,
∴∠ADB+∠GFD=90°,
∴∠CGD=90°,
∵∠FAE=90°,∠GCD=∠AEF,
∴△CGD∽△EAF,
∴
| CD |
| EF |
| CG |
| AE |
∴CD•AE=EF•CG.
故④正确,
故正确的有4个.
故选:D.
点评:此题主要考查了全等三角形的判定及性质、等腰直角三角形的判定与性质以及相似三角形的判定与性质;本题综合性强,难度较大,注意细心分析,熟练应用全等三角形的判定以及相似三角形的判定和性质是解决问题的关键.

练习册系列答案
相关题目
将多项式x2+4加上一个整式,使它成为完全平方式,则下列不满足条件的整式是( )
| A、-4 | ||
| B、±4x | ||
C、
| ||
D、
|
下列调查中,适宜采用普查的是( )
| A、了解宁德市空气质量情况 |
| B、了解闽江流域的水污染情况 |
| C、了解宁德市居民的环保意识 |
| D、了解全班同学每周体育锻炼的时间 |
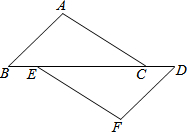 如图,已知点B,E,C,D在同一直线上,AB=FD,∠B=∠D,请你添加一个条件,使AC=FE,并给出证明(不再添加其它线段,不再标注或使用其他字母).你添加的条件是:
如图,已知点B,E,C,D在同一直线上,AB=FD,∠B=∠D,请你添加一个条件,使AC=FE,并给出证明(不再添加其它线段,不再标注或使用其他字母).你添加的条件是: 如图,数轴上表示1、
如图,数轴上表示1、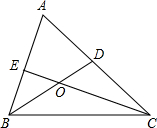 如图,△ABC的两条角平分线BD,CE交于点O
如图,△ABC的两条角平分线BD,CE交于点O 如图,在?ABCD中,AB=BK,直线KD与BC交于点E.求证:△ADK的周长为△ECD周长的两倍.
如图,在?ABCD中,AB=BK,直线KD与BC交于点E.求证:△ADK的周长为△ECD周长的两倍.