题目内容
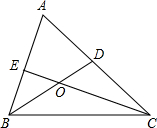 如图,△ABC的两条角平分线BD,CE交于点O
如图,△ABC的两条角平分线BD,CE交于点O(1)若∠ABC=70°,∠ACB=50°,求∠BOC的度数;
(2)若∠A=70°,求∠BOC的度数.
考点:三角形内角和定理,三角形的外角性质
专题:
分析:(1)先根据角平分线的性质求出∠OBC与∠OCB的度数,再由三角形内角和定理即可得出结论;
(2)先根据三角形内角和定理求出∠ABC+∠ACB的度数,再由角平分线的性质得出∠OBC+∠OCB的度数,进而可得出结论.
(2)先根据三角形内角和定理求出∠ABC+∠ACB的度数,再由角平分线的性质得出∠OBC+∠OCB的度数,进而可得出结论.
解答:解:(1)∵∠ABC=70°,∠ACB=50°,△ABC的两条角平分线BD,CE交于点O,
∴∠OBC=
∠ABC=35°,∠OCB=
∠ACB=25°,
∴∠BOC=180°-35°-25°=120°;
(2)∵∠A=70°,
∴∠ABC+∠ACB=180°-70°=110°.
∵△ABC的两条角平分线BD,CE交于点O,
∴∠OBC+∠OCB=
×110°=55°,
∴∠BOC=180°-55°=125°.
∴∠OBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BOC=180°-35°-25°=120°;
(2)∵∠A=70°,
∴∠ABC+∠ACB=180°-70°=110°.
∵△ABC的两条角平分线BD,CE交于点O,
∴∠OBC+∠OCB=
| 1 |
| 2 |
∴∠BOC=180°-55°=125°.
点评:本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目
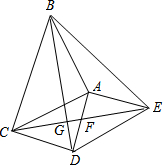 如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连接CE交AD于点F,连接BD交CE于点G,连接BE;下列结论中:①CE=BD;②∠ADB=∠AEB;③△ADC是等腰直角三角形;④CD•AE=EF•CG;一定正确的结论有( )
如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连接CE交AD于点F,连接BD交CE于点G,连接BE;下列结论中:①CE=BD;②∠ADB=∠AEB;③△ADC是等腰直角三角形;④CD•AE=EF•CG;一定正确的结论有( )| A、1个 | B、2个 | C、3个 | D、4个 |
 实数a,b在数轴上的位置如图所示,则式子
实数a,b在数轴上的位置如图所示,则式子| a2 |
| b2 |
| A、a+b | B、a-b |
| C、-a-b | D、-a+b |
 如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠PEF的度数是( )
如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠PEF的度数是( )| A、15° | B、20° |
| C、25° | D、30° |
下列说法中,正确的是( )
| A、直线虽然没有端点,但长度是可以度量的 |
| B、射线只有一个端点,但长度却是可以确定的 |
| C、线段虽然有两个端点,但长度却是可以变化的 |
| D、只有线段的长度是可以确定的,直线、射线的长度不可以度量 |
 观察函数y=
观察函数y= 如图,是某物体的主视图和俯视图,依据此物体的主视图和俯视图找出符合该物体的左视图( )
如图,是某物体的主视图和俯视图,依据此物体的主视图和俯视图找出符合该物体的左视图( )


