题目内容
将多项式x2+4加上一个整式,使它成为完全平方式,则下列不满足条件的整式是( )
| A、-4 | ||
| B、±4x | ||
C、
| ||
D、
|
考点:完全平方式
专题:
分析:分x2是平方项与乘积二倍项,以及单项式的平方三种情况,根据完全平方公式讨论求解.
解答:解:①当x2是平方项时,4±4x+x2=(2±x)2,
则可添加的项是4x或-4x,
②当x2是乘积二倍项时,4+x2+
x4=(2+
x2)2,
则可添加的项是
x4.
③添加-4或-x2.
故选:D.
则可添加的项是4x或-4x,
②当x2是乘积二倍项时,4+x2+
| 1 |
| 16 |
| 1 |
| 16 |
则可添加的项是
| 1 |
| 16 |
③添加-4或-x2.
故选:D.
点评:本题考查了完全平方式,比较复杂,需要我们全面考虑问题,首先考虑三个项分别充当中间项的情况,就有三种情况,还有就是第四种情况加上一个数,得到一个单独的单项式,也是可以成为一个完全平方式,这种情况比较容易忽略,要注意.

练习册系列答案
相关题目
用配方法解方程x2-2x-1=0时,配方后所得的方程为( )
| A、(x-1)2=2 |
| B、(x-1)2=0 |
| C、(x+1)2=2 |
| D、(x+1)2=0 |
 如图,∠1+∠3=180°,试说明:AB∥CD.
如图,∠1+∠3=180°,试说明:AB∥CD.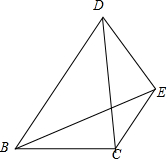 在△ABC中,BC=CD,∠BCD=90°,E是△BCD外一点,CE∥BD,且BE=BD,求
在△ABC中,BC=CD,∠BCD=90°,E是△BCD外一点,CE∥BD,且BE=BD,求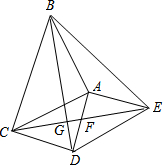 如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连接CE交AD于点F,连接BD交CE于点G,连接BE;下列结论中:①CE=BD;②∠ADB=∠AEB;③△ADC是等腰直角三角形;④CD•AE=EF•CG;一定正确的结论有( )
如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连接CE交AD于点F,连接BD交CE于点G,连接BE;下列结论中:①CE=BD;②∠ADB=∠AEB;③△ADC是等腰直角三角形;④CD•AE=EF•CG;一定正确的结论有( )