题目内容
 如图,在?ABCD中,AB=BK,直线KD与BC交于点E.求证:△ADK的周长为△ECD周长的两倍.
如图,在?ABCD中,AB=BK,直线KD与BC交于点E.求证:△ADK的周长为△ECD周长的两倍.考点:平行四边形的性质
专题:证明题
分析:由条件可证明E为DK的中点,可得BE=
AD,可知E为BC中点,结合平行四边形的性质,可证得结论.
| 1 |
| 2 |
解答:证明:∵四边形ABCD为平行四边形,
∴AD∥BC,且AD=BC,AB=CD,
∵AB=BK,
∴KE=ED,即KD=2DE,
∴BE为△AKD的中位线,
∴AD=2BE,
又∵AD=BC,
∴AD=EC,
且AK=2AB=2CD,
∴AK+AD+KD=2DC+2EC+2DE=2(DC+EC+DE),
即△ADK的周长为△ECD周长的两倍.
∴AD∥BC,且AD=BC,AB=CD,
∵AB=BK,
∴KE=ED,即KD=2DE,
∴BE为△AKD的中位线,
∴AD=2BE,
又∵AD=BC,
∴AD=EC,
且AK=2AB=2CD,
∴AK+AD+KD=2DC+2EC+2DE=2(DC+EC+DE),
即△ADK的周长为△ECD周长的两倍.
点评:本题主要考查平行四边形的性质,掌握平行四边形的对边平行且相等是解题的关键.

练习册系列答案
相关题目
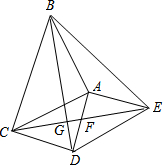 如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连接CE交AD于点F,连接BD交CE于点G,连接BE;下列结论中:①CE=BD;②∠ADB=∠AEB;③△ADC是等腰直角三角形;④CD•AE=EF•CG;一定正确的结论有( )
如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连接CE交AD于点F,连接BD交CE于点G,连接BE;下列结论中:①CE=BD;②∠ADB=∠AEB;③△ADC是等腰直角三角形;④CD•AE=EF•CG;一定正确的结论有( )| A、1个 | B、2个 | C、3个 | D、4个 |
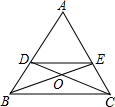 在△ABC中,AB=AC,BE,CD分别是∠ABC,∠ACB的平分线,则下列结论不正确的是( )
在△ABC中,AB=AC,BE,CD分别是∠ABC,∠ACB的平分线,则下列结论不正确的是( )| A、△OBC是等腰三角形 |
| B、△DBE是等腰三角形 |
| C、△DCE是等腰三角形 |
| D、△ACD是等腰三角形 |
下列说法中,正确的是( )
| A、直线虽然没有端点,但长度是可以度量的 |
| B、射线只有一个端点,但长度却是可以确定的 |
| C、线段虽然有两个端点,但长度却是可以变化的 |
| D、只有线段的长度是可以确定的,直线、射线的长度不可以度量 |
 如图是由四个完全相同的正方体组成的几何体,这个几何体的左视图是( )
如图是由四个完全相同的正方体组成的几何体,这个几何体的左视图是( )A、 |
B、 |
C、 |
D、 |
 如图,是某物体的主视图和俯视图,依据此物体的主视图和俯视图找出符合该物体的左视图( )
如图,是某物体的主视图和俯视图,依据此物体的主视图和俯视图找出符合该物体的左视图( )



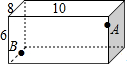 如图所示,在长、宽、高分别为10cm、8cm、6cm的长方体器皿的A点(三等分点)有一只蚂蚁,在B点(四等分点)处有一粒大米,请计算:蚂蚁要吃到大米最少要走多远.
如图所示,在长、宽、高分别为10cm、8cm、6cm的长方体器皿的A点(三等分点)有一只蚂蚁,在B点(四等分点)处有一粒大米,请计算:蚂蚁要吃到大米最少要走多远.