题目内容
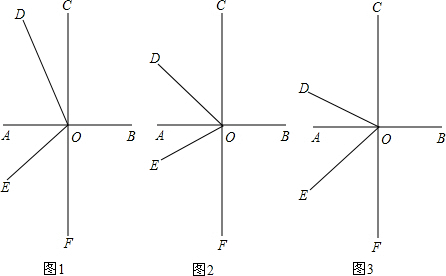
如图,O为直线AB与直线CF的交点,∠BOC=α.
(1)如图1所示,若α=40°,OD平分∠AOC,∠DOE=90°,求∠EOF的度数;
(2)如图2所示,若∠AOD=
∠AOC,∠DOE=45°,试求∠EOF的度数;(注意:∠BOC=α)
(3)如图3所示,若∠AOD=
∠AOC,∠DOE=
,n≥2,且n为正整数,猜想∠EOF与α的数量关系是 (直接写出结果,不要求写过程)
(1)如图1所示,若α=40°,OD平分∠AOC,∠DOE=90°,求∠EOF的度数;
(2)如图2所示,若∠AOD=
| 1 |
| 4 |
(3)如图3所示,若∠AOD=
| 1 |
| n |
| 180° |
| n |

考点:对顶角、邻补角,角的计算
专题:
分析:(1)先求出∠AOF=∠BOC=40°,再求出∠AOD=
∠AOC=70°,∠AOE=20°,即可求出∠EOF=20°;
(2)设∠AOD为x,则∠AOC=4x,由∠AOD+∠BOC=180°,得出x=45°-
,即可得出∠EOF=180°-∠DOE-∠COD=
α;
(3)设∠AOD为x,则∠AOC=nx,根据∠AOD+∠BOC=180°,列出方程:nx+α=180°,求出x,再由对顶角求出∠AOF=∠BOC=α,求出∠AOE=∠DOE-x═
,即可得出结论∠EOF=
.
| 1 |
| 2 |
(2)设∠AOD为x,则∠AOC=4x,由∠AOD+∠BOC=180°,得出x=45°-
| α |
| 4 |
| 3 |
| 4 |
(3)设∠AOD为x,则∠AOC=nx,根据∠AOD+∠BOC=180°,列出方程:nx+α=180°,求出x,再由对顶角求出∠AOF=∠BOC=α,求出∠AOE=∠DOE-x═
| α |
| n |
| (n-1)α |
| n |
解答:解:(1)∵α=40°,
∴∠AOC=180°-40°=140°,∠AOF=∠BOC=40°,
∵OD平分∠AOC,
∴∠AOD=
∠AOC=70°,
∵∠DOE=90°,
∴∠AOE=90°-70°=20°,
∴∠EOF=40°-20°=20°;
(2)设∠AOD为x,则∠AOC=4x,
∵∠AOD+∠BOC=180°,
∴4x+α=180°,
∴x=45°-
,
∴∠COD=3x=135°-
α,
∴∠EOF=180°-∠DOE-∠COD=180°-45°-(135°-
α)=
α;
(3)∠EOF与α的数量关系为:∠EOF=
;
设∠AOD为x,则∠AOC=nx,
∵∠AOD+∠BOC=180°,
∴nx+α=180°,
∴x=
-
,
∵∠AOF=∠BOC=α,∠AOE=∠DOE-x=
-(
-
)=
,
∴∠EOF=α-
=
故答案为:∠EOF=
.
∴∠AOC=180°-40°=140°,∠AOF=∠BOC=40°,
∵OD平分∠AOC,
∴∠AOD=
| 1 |
| 2 |
∵∠DOE=90°,
∴∠AOE=90°-70°=20°,
∴∠EOF=40°-20°=20°;
(2)设∠AOD为x,则∠AOC=4x,
∵∠AOD+∠BOC=180°,
∴4x+α=180°,
∴x=45°-
| α |
| 4 |
∴∠COD=3x=135°-
| 3 |
| 4 |
∴∠EOF=180°-∠DOE-∠COD=180°-45°-(135°-
| 3 |
| 4 |
| 3 |
| 4 |
(3)∠EOF与α的数量关系为:∠EOF=
| (n-1)α |
| n |
设∠AOD为x,则∠AOC=nx,
∵∠AOD+∠BOC=180°,
∴nx+α=180°,
∴x=
| 180° |
| n |
| α |
| n |
∵∠AOF=∠BOC=α,∠AOE=∠DOE-x=
| 180° |
| n |
| 180° |
| n |
| α |
| n |
| α |
| n |
∴∠EOF=α-
| α |
| n |
| (n-1)α |
| n |
故答案为:∠EOF=
| (n-1)α |
| n |
点评:本题考查了对顶角、邻补角以及角平分线的定义、角的计算;弄清各个角之间的关系,熟练掌握角的计算是解题的关键.

练习册系列答案
相关题目
刘谦的魔术表演风靡全国,小明也学起了刘谦的发明了一个魔术盒,当任意有理数对(a,b)进入其中时,会得到一个新的有理数:a-b2+1,例如:把(3,-2)放入其中,就会得到3-(-2)2+1=0,现将有理数对(0,-3)放入其中,则会得到( )
| A、10 | B、-9 | C、-8 | D、-7 |
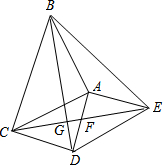 如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连接CE交AD于点F,连接BD交CE于点G,连接BE;下列结论中:①CE=BD;②∠ADB=∠AEB;③△ADC是等腰直角三角形;④CD•AE=EF•CG;一定正确的结论有( )
如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连接CE交AD于点F,连接BD交CE于点G,连接BE;下列结论中:①CE=BD;②∠ADB=∠AEB;③△ADC是等腰直角三角形;④CD•AE=EF•CG;一定正确的结论有( )| A、1个 | B、2个 | C、3个 | D、4个 |
 如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠PEF的度数是( )
如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠PEF的度数是( )| A、15° | B、20° |
| C、25° | D、30° |
 如图所示为“贾宪三角”的一部分,也称“杨辉三角系数表”,它的作用是指导我们按规律写出形如(a+b)″(其中n为正整数)的展开式中各项的系数,请你仔细观察图中的规律,填写下面(a+b)4,(a+b)5展开式中所缺的系数
如图所示为“贾宪三角”的一部分,也称“杨辉三角系数表”,它的作用是指导我们按规律写出形如(a+b)″(其中n为正整数)的展开式中各项的系数,请你仔细观察图中的规律,填写下面(a+b)4,(a+b)5展开式中所缺的系数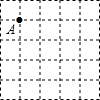 在5×5的正方形方格中,每个小正方形的边长都为1,请在下图给定的网格中按下列要求画出图形.
在5×5的正方形方格中,每个小正方形的边长都为1,请在下图给定的网格中按下列要求画出图形. 有下列四个判断:①AD=BF;②AE=BC;③∠EFA=∠CDB;④AE∥BC.请你以其中三个作为题设,余下一个作为结论,写出一个真命题并加以证明.
有下列四个判断:①AD=BF;②AE=BC;③∠EFA=∠CDB;④AE∥BC.请你以其中三个作为题设,余下一个作为结论,写出一个真命题并加以证明.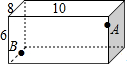 如图所示,在长、宽、高分别为10cm、8cm、6cm的长方体器皿的A点(三等分点)有一只蚂蚁,在B点(四等分点)处有一粒大米,请计算:蚂蚁要吃到大米最少要走多远.
如图所示,在长、宽、高分别为10cm、8cm、6cm的长方体器皿的A点(三等分点)有一只蚂蚁,在B点(四等分点)处有一粒大米,请计算:蚂蚁要吃到大米最少要走多远.