题目内容
15. 如图,四边形ABCD内接于⊙O,AD、BC的延长线相交于点E,AB、DC的延长线相交于点F.若∠E+∠F=70°,则∠A=55°.
如图,四边形ABCD内接于⊙O,AD、BC的延长线相交于点E,AB、DC的延长线相交于点F.若∠E+∠F=70°,则∠A=55°.
分析 根据圆内接四边形的性质得到∠ADC=∠FBC,根据三角形内角和定理得到∠ADC=180°-∠A-∠F,根据三角形的外角的性质得到∠FBC=∠A+∠E,列式计算即可.
解答 解:∵四边形ABCD内接于⊙O,
∴∠ADC=∠FBC,
∵∠ADC=180°-∠A-∠F,∠FBC=∠A+∠E,
∴180°-∠A-∠F=∠A+∠E,
则2∠A=180°-(∠F+∠E)=110°,
解得,∠A=55°,
故答案为:55°.
点评 本题考查的是圆内接四边形的性质和三角形的外角的性质,掌握圆内接四边形的任意一个外角等于它的内对角是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.把抛物线y=x2-3向右平移2个单位,然后向上平移2个单位,则平移后得到的抛物线的解析式为( )
| A. | y=(x-2)2-1 | B. | y=(x+2)2-1 | C. | y=(x-2)2+1 | D. | y=(x+2)2+1 |
7. 我区为了解七年级学生的环保意识,在全区范围内组织七年级学生进行了一次环保知识测试,随机抽取了若干名学生的成绩(成绩为整数,满分100分),进行统计后,绘制出如下频数分布表和如图所示不完整的频数分布直方图.
我区为了解七年级学生的环保意识,在全区范围内组织七年级学生进行了一次环保知识测试,随机抽取了若干名学生的成绩(成绩为整数,满分100分),进行统计后,绘制出如下频数分布表和如图所示不完整的频数分布直方图.
请根据图表信息回答下列问题:
(1)在频数分布表中,a=60,b=0.05.并补全频数分别直方图.
(2)甲同学说:“我的成绩是此次抽样调查所得数据的中位数”,问甲同学的成绩应在什么范围?
(3)全区共有七年级学生5000名,若规定成绩在80分以上(不含80分)为优秀,估计这次考试中成绩为优秀的学生有多少人?
 我区为了解七年级学生的环保意识,在全区范围内组织七年级学生进行了一次环保知识测试,随机抽取了若干名学生的成绩(成绩为整数,满分100分),进行统计后,绘制出如下频数分布表和如图所示不完整的频数分布直方图.
我区为了解七年级学生的环保意识,在全区范围内组织七年级学生进行了一次环保知识测试,随机抽取了若干名学生的成绩(成绩为整数,满分100分),进行统计后,绘制出如下频数分布表和如图所示不完整的频数分布直方图.| 成绩 | 频数 | 频率 |
| 50.5~60.5 | 20 | 0.1 |
| 60.5~70.5 | 40 | 0.2 |
| 70.5~80.5 | 70 | 0.35 |
| 80.5~90.5 | a | 0.3 |
| 90.5~100.5 | 10 | b |
(1)在频数分布表中,a=60,b=0.05.并补全频数分别直方图.
(2)甲同学说:“我的成绩是此次抽样调查所得数据的中位数”,问甲同学的成绩应在什么范围?
(3)全区共有七年级学生5000名,若规定成绩在80分以上(不含80分)为优秀,估计这次考试中成绩为优秀的学生有多少人?
4.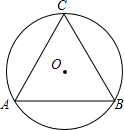 如图,等边△ABC是⊙O的内接三角形,则圆心O关于直线AB的对称点O′和⊙O的位置关系是( )
如图,等边△ABC是⊙O的内接三角形,则圆心O关于直线AB的对称点O′和⊙O的位置关系是( )
 如图,等边△ABC是⊙O的内接三角形,则圆心O关于直线AB的对称点O′和⊙O的位置关系是( )
如图,等边△ABC是⊙O的内接三角形,则圆心O关于直线AB的对称点O′和⊙O的位置关系是( )| A. | 在⊙O内 | B. | 在⊙O上 | C. | 在⊙O外 | D. | 不能确定 |
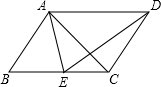 如图,在?ABCD中,E为BC边上一点,且AB=AE,若AE平分∠DAB,∠EAC=25°,则∠AED的度数是85度.
如图,在?ABCD中,E为BC边上一点,且AB=AE,若AE平分∠DAB,∠EAC=25°,则∠AED的度数是85度.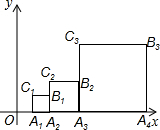 如图,正方形A1A2B1C1,A2A3B2C2,…Anan+1BnCn,如图位置依次摆放,已知点C1,C2,C3…,Cn在直线y=x上,点A1的坐标为(1,0).
如图,正方形A1A2B1C1,A2A3B2C2,…Anan+1BnCn,如图位置依次摆放,已知点C1,C2,C3…,Cn在直线y=x上,点A1的坐标为(1,0).