题目内容
20.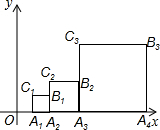 如图,正方形A1A2B1C1,A2A3B2C2,…Anan+1BnCn,如图位置依次摆放,已知点C1,C2,C3…,Cn在直线y=x上,点A1的坐标为(1,0).
如图,正方形A1A2B1C1,A2A3B2C2,…Anan+1BnCn,如图位置依次摆放,已知点C1,C2,C3…,Cn在直线y=x上,点A1的坐标为(1,0).(1)写出正方形A1A2B1C1,A2A3B2C2,…Anan+1BnCn,的位似中心坐标;
(2)正方形A4A3B4C4四个顶点的坐标.
分析 (1)直接利用位似图形的性质得出对应点连线的交点为原点,进而得出答案;
(2)利用一次函数图象上点的坐标性质得出各线段的长,进而得出答案.
解答  解:(1)如图所示:正方形A1A2B1C1,A2A3B2C2,A3A4B3C3,…,AnAn+1BnCn的位似中心坐标为:(0,0);
解:(1)如图所示:正方形A1A2B1C1,A2A3B2C2,A3A4B3C3,…,AnAn+1BnCn的位似中心坐标为:(0,0);
(2)∵点C1,C2,C3,…,Cn在直线y=x上,点A1的坐标为(1,0),
∴OA1=A1C1=1,OA2=A2C2=2,则A3O=A3C3=4,
∴可得:OA4=A4C4=8,
则OA5=16,
故A4(8,0),A5(16,0),B4(16,8),C4(8,8).
点评 此题主要考查了位似变换以及一次函数图象上点的坐标特点以及正方形的性质,正确得出各线段的长是解题关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
12.下列各式中,无意义的是( )
| A. | $\sqrt{-{2^2}}$ | B. | $\root{3}{{-{2^2}}}$ | C. | $\sqrt{{{(-2)}^2}}$ | D. | $\root{3}{{{{(-2)}^2}}}$ |
 如图,在矩形ABCD中,AB=8,AD=12,过点A、D两点的⊙O与BC边相切于点E,则⊙O的半径为$\frac{25}{4}$.
如图,在矩形ABCD中,AB=8,AD=12,过点A、D两点的⊙O与BC边相切于点E,则⊙O的半径为$\frac{25}{4}$.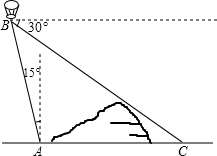 如图,在小山的西侧A处有一热气球,以25米/分钟的速度沿着与垂直方向所成夹角为15°的方向升空,40分钟后到达B处,这时热气球上的人发现,在A处的正东方向有一处着火点C,在B处测得着火点C的俯角为30°,求热气球升空点A与着火点C的距离.(结果保留根号)
如图,在小山的西侧A处有一热气球,以25米/分钟的速度沿着与垂直方向所成夹角为15°的方向升空,40分钟后到达B处,这时热气球上的人发现,在A处的正东方向有一处着火点C,在B处测得着火点C的俯角为30°,求热气球升空点A与着火点C的距离.(结果保留根号) 如图,四边形ABCD内接于⊙O,AD、BC的延长线相交于点E,AB、DC的延长线相交于点F.若∠E+∠F=70°,则∠A=55°.
如图,四边形ABCD内接于⊙O,AD、BC的延长线相交于点E,AB、DC的延长线相交于点F.若∠E+∠F=70°,则∠A=55°. 如图,菱形ABCD中,对角线AC、BD交于点O,E为AD边中点,菱形ABCD的周长为24,则OE的长等于( )
如图,菱形ABCD中,对角线AC、BD交于点O,E为AD边中点,菱形ABCD的周长为24,则OE的长等于( )