题目内容
5.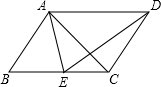 如图,在?ABCD中,E为BC边上一点,且AB=AE,若AE平分∠DAB,∠EAC=25°,则∠AED的度数是85度.
如图,在?ABCD中,E为BC边上一点,且AB=AE,若AE平分∠DAB,∠EAC=25°,则∠AED的度数是85度.
分析 先证明∠B=∠EAD,然后利用SAS证明△ABC≌△EAD,得出∠AED=∠BAC.再证明△ABE为等边三角形,可得∠BAE=60°,求出∠BAC的度数,即可得∠AED的度数.
解答 解:∵在平行四边形ABCD中,AD∥BC,BC=AD,
∴∠EAD=∠AEB,
又∵AB=AE,
∴∠B=∠AEB,
∴∠B=∠EAD,
在△ABC和△EAD中,$\left\{\begin{array}{l}{AB=AE}&{\;}\\{∠ABC=∠EAD}&{\;}\\{BC=AD}&{\;}\end{array}\right.$,
∴△ABC≌△EAD(SAS),
∴∠AED=∠BAC.
∵AE平分∠DAB,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB=∠B,
∴△ABE为等边三角形,
∴∠BAE=60°,
∴∠BAC=∠BAE+∠EAC=85°,
∴∠AED=∠BAC=85°;
故答案为:85.
点评 本题考查了平行四边形的性质、全等三角形的判定与性质,等边三角形的判定与性质;熟记平行四边形的性质,证明三角形全等和等边三角形是解决问题的关键.

练习册系列答案
相关题目
16.计算6×(-2)-12÷(-4)的结果是( )
| A. | 10 | B. | 0 | C. | -3 | D. | -9 |
 如图,在平面直角坐标系中,Rt△OAB的顶点B在x轴的正半轴上,已知∠OBA=90°,OB=3,sin∠AOB=$\frac{4}{5}$.反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A.
如图,在平面直角坐标系中,Rt△OAB的顶点B在x轴的正半轴上,已知∠OBA=90°,OB=3,sin∠AOB=$\frac{4}{5}$.反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A. 如图,在直升机的镜头下,观测A处的俯角为30°,B处的俯角为45°.如果此时直升机镜头C处的高度CD为200米,点A、D、B在同一直线上,则AB两点的距离是200($\sqrt{3}$+1)米.
如图,在直升机的镜头下,观测A处的俯角为30°,B处的俯角为45°.如果此时直升机镜头C处的高度CD为200米,点A、D、B在同一直线上,则AB两点的距离是200($\sqrt{3}$+1)米. 如图,在矩形ABCD中,AB=8,AD=12,过点A、D两点的⊙O与BC边相切于点E,则⊙O的半径为$\frac{25}{4}$.
如图,在矩形ABCD中,AB=8,AD=12,过点A、D两点的⊙O与BC边相切于点E,则⊙O的半径为$\frac{25}{4}$.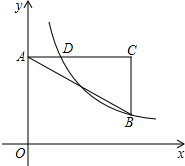 如图在直角坐标系中,点A在y轴正半轴上,AC∥x轴,点B,C的横坐标都是3,且BC=2,点D在AC上且横坐标为1,若反比例函数y=$\frac{k}{x}$(x>0)图象象经过点B,D,求k的值.
如图在直角坐标系中,点A在y轴正半轴上,AC∥x轴,点B,C的横坐标都是3,且BC=2,点D在AC上且横坐标为1,若反比例函数y=$\frac{k}{x}$(x>0)图象象经过点B,D,求k的值. 如图,四边形ABCD内接于⊙O,AD、BC的延长线相交于点E,AB、DC的延长线相交于点F.若∠E+∠F=70°,则∠A=55°.
如图,四边形ABCD内接于⊙O,AD、BC的延长线相交于点E,AB、DC的延长线相交于点F.若∠E+∠F=70°,则∠A=55°.