题目内容
7. 我区为了解七年级学生的环保意识,在全区范围内组织七年级学生进行了一次环保知识测试,随机抽取了若干名学生的成绩(成绩为整数,满分100分),进行统计后,绘制出如下频数分布表和如图所示不完整的频数分布直方图.
我区为了解七年级学生的环保意识,在全区范围内组织七年级学生进行了一次环保知识测试,随机抽取了若干名学生的成绩(成绩为整数,满分100分),进行统计后,绘制出如下频数分布表和如图所示不完整的频数分布直方图.| 成绩 | 频数 | 频率 |
| 50.5~60.5 | 20 | 0.1 |
| 60.5~70.5 | 40 | 0.2 |
| 70.5~80.5 | 70 | 0.35 |
| 80.5~90.5 | a | 0.3 |
| 90.5~100.5 | 10 | b |
(1)在频数分布表中,a=60,b=0.05.并补全频数分别直方图.
(2)甲同学说:“我的成绩是此次抽样调查所得数据的中位数”,问甲同学的成绩应在什么范围?
(3)全区共有七年级学生5000名,若规定成绩在80分以上(不含80分)为优秀,估计这次考试中成绩为优秀的学生有多少人?
分析 (1)首先根据第一组的已知频数与已知频率计算出抽取的学生总数,然后根据频数、频率与数据总数之间的关系求出a、b的值,最后补全频数分布直方图;
(2)根据中位数的定义即可求解;
(3)80分以上(不含80分)的学生数就是第四、五组的学生数之和,将样本中这两组的频率相加,乘以全区七年级学生总人数即可求解.
解答 解:(1)抽取的学生总数为:20÷0.1=200.
a=200×0.3=60,b=$\frac{10}{200}$=0.05.
补全的频数分布直方图如下:
(2)∵一共有200个数据,按从小到大的顺序排列后,第100与101个数都落在第三组:70.5~80.5,
∴此次抽样调查所得数据的中位数是70.5~80.5,
∴甲同学的成绩所在范围是70.5~80.5;
(3)这次考试中成绩为优秀的学生为:5000(0.3+0.05)=1750人.
故答案为60,0.05.
点评 本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
18. 在信息快速发展的社会,“信息消费”已成为人们生活的重要组成部分.某高校组织课外小组在郑州市的一个社区随机抽取部分家庭,调查每月用于信息消费的金额,根据数据整理成如图所示的不完整统计表和统计图.已知A,B两组户数频数直方图的高度比为1:5.
在信息快速发展的社会,“信息消费”已成为人们生活的重要组成部分.某高校组织课外小组在郑州市的一个社区随机抽取部分家庭,调查每月用于信息消费的金额,根据数据整理成如图所示的不完整统计表和统计图.已知A,B两组户数频数直方图的高度比为1:5.
月信息消费额分组统计表
请结合图表中相关数据解答下列问题:
(1)这次接受调查的有50户;
(2)在扇形统计图中,“E”所对应的圆心角的度数是28.8°;
(3)请你补全频数直方图;
(4)若该社区有2000户住户,请估计月信息消费额不少于200元的户数是多少?
 在信息快速发展的社会,“信息消费”已成为人们生活的重要组成部分.某高校组织课外小组在郑州市的一个社区随机抽取部分家庭,调查每月用于信息消费的金额,根据数据整理成如图所示的不完整统计表和统计图.已知A,B两组户数频数直方图的高度比为1:5.
在信息快速发展的社会,“信息消费”已成为人们生活的重要组成部分.某高校组织课外小组在郑州市的一个社区随机抽取部分家庭,调查每月用于信息消费的金额,根据数据整理成如图所示的不完整统计表和统计图.已知A,B两组户数频数直方图的高度比为1:5.月信息消费额分组统计表
| 组别 | 消费额(元) |
| A | 10≤x<100 |
| B | 100≤x<200 |
| C | 20≤x<300 |
| D | 300≤x<400 |
| E | x≥400 |
(1)这次接受调查的有50户;
(2)在扇形统计图中,“E”所对应的圆心角的度数是28.8°;
(3)请你补全频数直方图;
(4)若该社区有2000户住户,请估计月信息消费额不少于200元的户数是多少?
12.下列各式中,无意义的是( )
| A. | $\sqrt{-{2^2}}$ | B. | $\root{3}{{-{2^2}}}$ | C. | $\sqrt{{{(-2)}^2}}$ | D. | $\root{3}{{{{(-2)}^2}}}$ |
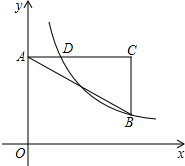 如图在直角坐标系中,点A在y轴正半轴上,AC∥x轴,点B,C的横坐标都是3,且BC=2,点D在AC上且横坐标为1,若反比例函数y=$\frac{k}{x}$(x>0)图象象经过点B,D,求k的值.
如图在直角坐标系中,点A在y轴正半轴上,AC∥x轴,点B,C的横坐标都是3,且BC=2,点D在AC上且横坐标为1,若反比例函数y=$\frac{k}{x}$(x>0)图象象经过点B,D,求k的值. 如图,四边形ABCD内接于⊙O,AD、BC的延长线相交于点E,AB、DC的延长线相交于点F.若∠E+∠F=70°,则∠A=55°.
如图,四边形ABCD内接于⊙O,AD、BC的延长线相交于点E,AB、DC的延长线相交于点F.若∠E+∠F=70°,则∠A=55°.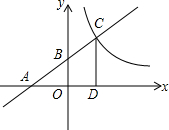 已知函数y1=$\frac{2}{3}$x+2的图象分别与坐标轴相交于A,B两点(如图所示),与反比例函数y2=$\frac{k}{x}$(x>0)的图象相交于C点.
已知函数y1=$\frac{2}{3}$x+2的图象分别与坐标轴相交于A,B两点(如图所示),与反比例函数y2=$\frac{k}{x}$(x>0)的图象相交于C点.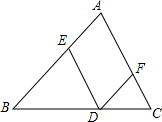 已知D为△ABC边BC上的一个动点(不与B,C重合),过D作DE∥AC交AB于点E,作DF∥AB交AC于点F.
已知D为△ABC边BC上的一个动点(不与B,C重合),过D作DE∥AC交AB于点E,作DF∥AB交AC于点F.