题目内容
4．
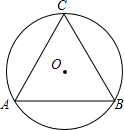如图，等边△ABC是⊙O的内接三角形，则圆心O关于直线AB的对称点O′和⊙O的位置关系是（ ）| A． | 在⊙O内 | B． | 在⊙O上 | C． | 在⊙O外 | D． | 不能确定 |
分析 连接OA，过点O作OD⊥AB，并作点O关于AB的对称点O′，设⊙O的半径为R，则OD=$\frac{1}{2}R$，可得OO′，利用圆和直线的位置关系可得结论．
解答 解：连接OA，过点O作OD⊥AB，并作点O关于AB的对称点O′，设⊙O的半径为R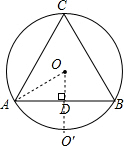
，
∵OD⊥AB，△ABC为正三角形，
则OD=AO•sin30°=$\frac{1}{2}$R，
∴OO′=R，
∴圆心O关于直线AB的对称点O′和⊙O的位置关系是在圆上，
故选B．
点评 本题主要考查了圆和直线的位置关系，掌握点与圆的位置关系有3种．设⊙O的半径为r，点P到圆心的距离OP=d，则有：①点P在圆外?d＞r；②点P在圆上?d=r；①点P在圆内?d＜r是解答此题的关键
练习册系列答案
阅读快车系列答案
相关题目
如图，四边形ABCD内接于⊙O，AD、BC的延长线相交于点E，AB、DC的延长线相交于点F．若∠E+∠F=70°，则∠A=55°．
12．下列各式中，无意义的是（ ）
| A． | $\sqrt{-{2^2}}$ | B． | $\root{3}{{-{2^2}}}$ | C． | $\sqrt{{{（-2）}^2}}$ | D． | $\root{3}{{{{（-2）}^2}}}$ |
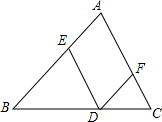已知D为△ABC边BC上的一个动点（不与B，C重合），过D作DE∥AC交AB于点E，作DF∥AB交AC于点F．
如图，菱形ABCD中，对角线AC、BD交于点O，E为AD边中点，菱形ABCD的周长为24，则OE的长等于（ ）